We’ve broken down this topic into three parts:
First, we cover what pain is and explore several different types of pain.
Next, we explore how kratom works for pain and what you need to know about dosing, tips for selecting the right type of kratom for different kinds of pain, and how to use it.
In the last section, we cover other effective approaches to managing pain.
I. Defining Pain
Pain is an uncomfortable physical and emotional experience, but it has a useful function.
The body uses the experience of pain to tell us when something is wrong and forces us to react. It’s a tool for self-preservation that helps us navigate life.
The best definition of pain comes from the Internal Association for the Study of Pain (IASP).
“[Pain is] an unpleasant sensory and emotional experience associated with, or resembling that associated with, actual or potential tissue damage.”
Everybody experiences pain differently according to various biological, psychological, and social factors. While there are well-known biological factors involved with the sensation of pain (such as nociception), there are emotional factors involved that make it futile to attempt to quantify pain based on the activation of sensory neurons.
There are plenty of examples of patients who experience pain but present no clear injury or underlying cause. Today, it’s a well-accepted fact that pain doesn’t necessarily need a specific physical cause to exist.
Pain can arise as a somatization of something purely psychological, just as much as it can represent physical injury or inflammation.
Why Do We Experience Pain?
In most cases, pain serves two simple purposes — adaptation and self-preservation. It signals when something is causing damage to the body and warns us to stay away from it in the future — like touching your hand on scalding metal or stroking a sharp knife. It also warns us when something is wrong so we can seek appropriate help to repair it.
So what would happen if we didn’t feel pain?
We can see how this would play out by looking at people suffering from Congenital Insensitivity to Pain and Anhidrosis (CIPA).
People with this syndrome cannot feel pain. This may sound like a superpower, but it’s extremely dangerous. Those diagnosed with the condition rarely reach the age of 25. Without being able to feel pain, sufferers don’t know when something is wrong and become especially prone to injuries.
It’s common for people with this condition to bite their tongues or brush their teeth so hard that their gums bleed.
Even worse, infections go unnoticed, and serious life-threatening injuries remain hidden.
Pain tells us to stop what we’re doing. If we break a bone, moving it around can cause the jagged edges to cause further damage to the surrounding tissue. When we have an infection, pain tells us to seek help before it worsens. When our muscles are sore, pain tells us to avoid hitting the gym until the muscles are repaired.
Our ability to feel pain is both a blessing and a curse.
Learn More: Why Do We Feel Pain?

Acute Pain vs. Chronic Pain
Acute and chronic pain are distinct types of pain that can differ in intensity, duration, and underlying causes.
Acute pain refers to pain that comes on suddenly and is typically temporary. This type of pain is normally caused by some kind of injury and goes away once the underlying problem is resolved.
Chronic pain persists for a long time — usually longer than six weeks or beyond the expected healing time of the original injury. Many factors can correspond to chronic pain, including various medical conditions, physical injuries, and psychological factors.
In many cases, chronic pain is a negative feedback loop. The key to managing it comes down to whether or not we can break this cycle.
For example, many people experience chronic pain due to a dysfunctional inflammatory response. The inflammation causes damage to the tissue, which leads to more inflammation — and the cycle continues. Over time, persistent inescapable pain starts affecting the mind as well. We lose motivation to move around and exercise, the quality of our sleep suffers, and we become isolated and depressed. All of these factors make us progressively more sensitive to pain.
Types of Pain You Should Never Ignore
Not all pain carries the same weight. Some forms of pain merely suggest taking some time to rest up or take it easy on a particular muscle or joint — others are a warning sign that something much more serious is going on.
Here are 8 types of pain you should never ignore:
- Chest Pain
- Intense Pain In One Calf or Thigh
- Intense Pain in Your Big Toe or Tip of the Nose
- Lower Back Pain
- Medication-Resistant Me
- Painful Urination
- Serious Headaches
- Severe Abdominal Pain
3 Types of Pain & How They Work
First of all, let’s differentiate between nociceptive pain (pain caused by the activation of the nociceptors), neuropathic pain (pain caused by damaged neurons), and nociplastic pain (pain that is not caused by the nociceptors or neurons).
Nociceptive Pain
This form of pain begins with a particular type of receptor called the nociceptor. These receptors are located all around the body and are designed to tell us when something is wrong.
Several different types of nociceptors detect different kinds of noxious stimuli (something that can damage the body’s integrity, such as tissue damage, pH changes, and temperature). They also detect chemical messengers (such as prostaglandins) that are released during the inflammatory process.
There are two main types of nociceptors:
- Alpha-Delta Fibers — these nociceptors are responsible for producing sharp, localized pain.
- C Fibers — these nociceptors produce slow, poorly localized burning or throbbing pain.
Once the nociceptors become active, they relay this information to the brain, where it can be interpreted and dealt with accordingly.
The signals generated in the nociceptors travel up the nerve axons as an electrical charge. They enter the back of the spinal cord. Once inside the spinal cord, the nociceptors transmit this signal to the second-order neurons by releasing chemical messengers such as the substance P.
Substance P (and other pain neurotransmitters) activate the second-order neurons, which carry this information into the brain.
The pain signal then arrives in the brain’s thalamus, which sorts the information and relays it to the associated area of the somatosensory cortex with the help of various neurotransmitters (dopamine, serotonin, and acetylcholine).
The area this signal is sent depends on which part of the body the pain was first detected.
Signs of Nociceptive Pain
- Pain with a clear underlying cause (injuries or chronic inflammation)
- Pain that is localized to a specific site
- Pain that is proportionate to the traumatic injury
- Pain that responds well to medications or herbal painkillers (such as kratom or CBD)
- Usually described as “sharp” pain
Neuropathic Pain
Neuropathic pain specifically refers to pain initiated by damage to the nerve fibers. Common causes of neuropathic pain include diabetes, infection (such as Herpes zoster), nerve compression, multiple sclerosis, and traumatic injuries to the neurons [9].
Neuropathic pain is differentiated from nociceptive pain because it doesn’t always require the activation of nociceptors to originate the pain signal. However, many experts believe the C-fibers (one of the main types of nociceptors) are responsible for initiating the neuropathic pain signal. This explains why neuropathic pain is generally non-localized (tough to identify the specific origin of the pain) and produces a slow-burning or throbbing sensation.
Most pain of neuropathic origin features similar characteristics:
- Burning or “electric” sensation
- Pain intensifies with light stroking of the skin
- Attacks of pain with little to no provocation
- Sensory deficits (reduced touch, hearing, vision, taste, or smell)
Signs of Neuropathic Pain
- Pain with a very high level of severity
- Pain that is usually worse at night
- History of nerve injuries or degenerative disease
- Less responsive to pain medications or herbal painkillers
- Pain is described as “burning,” “shooting,” or “throbbing”
- Other neurological symptoms usually present (pins and needles, numbness, weakness)
Psychosomatic or Nociplastic Pain
(Also known as functional pain disorder or chronic primary pain.)
Regardless of what you call it, many people experience chronic pain with no apparent link to actual damaged or threatened tissue.
There’s a lot of debate around what causes pain in people that don’t appear to have anything “physically” wrong with them. Some doctors and researchers argue this is merely caused by dysfunctional nociceptors (nociplastic pain), while others argue it’s a complex of various biopsychosocial factors (functional pain disorders) [11].
Some examples of psychosomatic pain syndromes include fibromyalgia, chronic back pain, interstitial cystitis, and complex regional pain syndrome (AKA functional pain disorder).
There’s a lot of disagreement around this topic in the medical community because this kind of pain is very hard to study and understand. There are no clear physiological factors or diagnostic tests to help us compare this kind of pain with other forms.
The only data point we have is that the patient is experiencing pain. We know pain is a personal experience; we can’t argue or assume that someone is simply “making it up.” The pain they experience is real regardless of whether or not there’s a clear physical cause for it or not.
For these people, it doesn’t matter how much diagnostic testing is done — there is no way to physically confirm the presence or cause of their pain.
This, of course, makes both research and treatment of psychosomatic pain extremely difficult.
At the moment, the leading theory is that psychosomatic pain is a complex biopsychosocial condition. It’s caused by a combination of biological factors (including dysfunctional nociceptors and differences in individual pain thresholds), psychological factors (such as mood disorders or alterations in neurotransmitter levels), and social components (such as childhood trauma and poor coping mechanisms).
Signs of Psychosomatic Pain
- The pain that is disproportionate to aggravating factors
- There is no clear underlying pathology to explain the source of the pain
- The pain may be described as either sharp or burning
- Other maladaptive disorders may also be present (chronic anxiety or depression)
- The pain is non-localized (pain felt in different areas of the body)
- The presence of pain may be associated with functional disabilities (interferes with work, school, or other responsibilities)
- The pain is unresponsive to medical treatment
- The pain tends to remain constant and chronic

II. Kratom For Pain
Few natural products on Earth can compete with the painkilling capacity of kratom (Mitragyna speciosa). Even herbs like turmeric, cannabis, and boswellia that have an excellent reputation as natural painkillers can’t hold a torch next to kratom in this regard.
Kratom and its active alkaloids primarily target the opiate receptors [1], which act as gatekeepers for pain signals as they travel up the spinal cord and into the brain. By activating these receptors, kratom alkaloids reduce the volume of these pain signals. This directly translates to a reduction in pain perception.
But kratom does much more than this.
Unlike conventional opiate-based painkillers, which have been the gold standard for pain management for nearly 200 years [2], kratom alkaloids are non-specific for the opiate receptors.
This means they interact synergistically with other key neurotransmitter systems in the brain and spinal cord too.
Several of these systems are directly linked with the sensation and interpretation of pain signals in the brain.
Others contribute to the analgesic profile of the plant less directly — such as corynoxine A and B, which offer neuroprotective effects to help repair damaged neurons, or corynanthine, which further reduces pain signal transduction by targeting the calcium ion channels of our neurons.
There are also elements that act as antioxidants, muscle relaxants, anti-inflammatories, and dopaminergic regulators present in kratom leaves that all work together to alleviate different kinds of pain.
One clinical trial found that a single dose of kratom significantly increased patients’ individual pain thresholds (the intensity of painful stimuli they were able to endure) [34].

Kratom For Pain: Mechanisms of Action
Unlike prescription painkillers, the many alkaloids in kratom treat pain differently — offering more well-rounded analgesic effects:
- Mu-, kappa-, and delta-opioid pain receptors — These receptors act as the primary gatekeepers for the pain signals traveling toward the brain. 7-hydroxymitragynine, mitragynine, and speciociliatine have the strongest action on these receptors.
- Adrenergic receptors — The ɑ1 and ɑ2 adrenergic receptors are involved in both the modulation and interpretation of pain signals in the brain. Adrenergic agonists are often used as alternative painkillers when opiate drugs are inappropriate.
- Calcium channels — Some alkaloids, such as corynanthine, have been shown to inhibit calcium ion channels. This action reduces pain signal transduction, and medications with this effect are sometimes used as an alternative option to opioid painkillers in the hospital setting.
- Dopamine — Ajmalicine and corynantheidine have the strongest impact on these neurotransmitters. Dopamine and serotonin are less involved with pain than the opiate receptors or adrenergic receptors, but both are involved with the interpretation and downstream effects pain has on the body.
- Serotonin — The exact role of serotonin in the pain response is not well understood, but studies have shown that increasing serotonin activity can reduce pain sensitivity and increase tolerance to pain. Isopteropodine and epicatechin have both been shown to modulate serotonergic function in the brain.
- COX, phosphodiesterase, and lipopolysaccharide — Mitraphylline, epicatechin, and rhynchophylline each interact with these various enzymes to limit inflammation and reduce chronic pain.
- Metabolic Competitors — Most alkaloids in kratom compete for the same liver enzymes tasked with breaking them down. This effect prolongs the duration of effects and enhances the potency of powerful kratom alkaloids such as 7-hydroxymitragynine.
- Neuroprotectants — Compounds like corynoxine A and corynoxine B act as neuroprotectants to support the recovery of damaged neurons that may be causing pain.
- Muscle Relaxants — Both mitraphylline & speciogynine act as a muscle-relaxants to support muscle tension-related pain.
All these pathways are involved in the transmission, interpretation, and somatic expression of pain in various ways.

What’s The Best Kratom Strain For Pain?
Not all kratom is created equal. Differences in alkaloid content and potency make some kratom strains better for managing pain than others.
The general rule of thumb is that red vein kratom — especially very strong red vein strains such as Maeng Da kratom — is the most effective for managing pain.
Most people who use kratom for pain use raw powder or extract tablets mixed with some warm water.
Best Kratom Strains For Pain
There are many different strains of kratom available on the market. Each one is unique based on where they were grown and how they were processed. These factors alter the ratio of mitragynine, 7-hydroxymitragynine, and other alkaloids in the final product.
Users can tailor kratom’s effects to match their health goals simply by selecting the right strain.
The general consensus regarding strain selection is that if you want the most pain-relief possible, go for a red vein kratom strain.
If you want relief from pain but find red vein strains a little too sedating, go for a strong green vein kratom strain instead.
White vein kratom strains still possess painkilling qualities, but it’s the weakest of the bunch. White vein kratom is normally used as a coffee alternative or mood-enhancer rather than a painkiller.
The best red vein strains for pain (in order) are Red Maeng Da, Red Bali, Red Malay, and Red Borneo.
The most popular green vein strains for managing pain are Green Malay, Green Borneo, and Green Maeng Da.
Some people will combine an energizing white vein kratom strain, such as White Dragon or White Kali Kratom, with a painkilling red vein strain to counter some of the sedative qualities.
Learn more about the best kratom strains for pain.

Kratom Dose For Pain: Dosing Considerations & Best Practices
The key to using kratom effectively comes down to two factors — the type of pain you’re trying to treat (as discussed above) and the dose.
Overall, the most common dose of kratom powder for managing pain is between 6 and 10 grams of powder.
With that said, everybody responds differently to kratom, so it’s important to take dosage guidelines with a grain of salt. These guidelines are here to help give you an idea of what dose you should be using, but it’s more important to listen to your body and adjust as needed.
If you take too much kratom, you’ll feel sick (nauseous, dizzy, fatigued) — and if you don’t take enough, your pain won’t go away. The trick is to find the dose that provides enough relief from pain without producing any of the unwanted side effects.
The best way to do this is to find your estimated dose using our kratom dosage calculator below.
You’ll need a good scale to accurately measure your kratom powder. If you don’t have a scale, you can also measure your kratom using tablespoons — but keep in mind that volumetric measurements are less reliable.
After you find your recommended dose, start with only half to see how your body responds. This is an important part of harm reduction when using kratom (or any herb) for the first time. This is done to make sure you aren’t allergic or overly sensitive to the effects of the plant.
After about an hour, if you feel fine, you can take the other half.
In general, you’ll want to wait at least 6 hours between doses. If you find the effects wear off too quickly, you can take smaller doses more frequently — but it’s wise to avoid consuming more than about 12 grams of kratom in one sitting, or 20 grams per day total.
Caution: Measuring kratom by volume is less accurate than weight. Use a scale.
As you use kratom for a few days, you’ll become accustomed to how your body responds. If you’re feeling fine with the dose you’re using but still have pain, increase by increments of about 10% until you feel the desired effects.
If you take a dose and feel nauseous or dizzy, it means you’ve gone too far and should take a lower dose next time.
Related: How Much Kratom is Too Much?
Kratom Onset Time
Kratom can take up to 1 hour before it kicks in, but most people will start to feel the effects closer to 30 minutes after taking it.
For muscle pain and autoimmune-related pain, you can expect this to take even longer. You may even need several doses (spread out over 24 or 48 hours, of course) before you experience sufficient relief from symptoms (more on this later).
When it comes to treating pain, there are three major factors that determine how long you’ll have to wait — these are the type of pain you’re experiencing, the state of your digestive health, and the type of kratom products you’re using.
Let’s cover each of these factors in more detail:
A) How The Type of Pain Affects Kratom’s Onset & Duration
As we covered in the first section, there are many different types of pain — not all forms of pain respond the same way to painkillers like kratom.
It comes down to the way kratom is absorbed and processed after you take it.
Kratom will first enter the stomach, where its active ingredients are gradually broken down and absorbed through the digestive tract. Once they’re in the bloodstream, these compounds need to circulate around the body (covering a distance of around 60,000 miles worth of blood vessels) before eventually reaching the target site.
Most of the painkilling action of kratom happens in the spinal cord and brain. The active alkaloids interact with the opiate receptors stationed here that act as gatekeepers for pain signals as they travel up the spinal cord and into the brain.
This means all forms of pain should experience at least some improvement within the first 30–60 minutes.
However, kratom also works to dull pain at the source of the pain too. Depending on where in the body the pain originates from, it can take more or less time for the active ingredients to reach the area.
For example, gout pain — which originates in the tip of the big toe, can take a while. This part of the body doesn’t experience much blood flow, so it can take a long time for the alkaloids to reach it and exert their analgesic action.
Conversely, pain in the digestive tract or pain originating in the muscles in the lower back is hit relatively quickly. Both of these areas are constantly bathed in fresh blood, which carries with it kratoms painkilling alkaloids.

B) How Your Digestive Health Affects Kratom’s Onset & Duration
This factor is more significant than you might think — most people don’t even take it into consideration, but it’s extremely relevant here.
People who have poor digestion (either not enough stomach acid, excessive inflammation in the intestines, a lack of pancreatic enzymes, poor microbiome status, or a combination of them all) report both a slower onset of effects and less potency overall compared to people with strong digestion.
Think about it. As a herb, kratom needs to be broken down before the active ingredients can be absorbed into the body. If digestion is weak, it could block or slow the ability of the active painkilling ingredients to enter the body and exert their effects.
One simple solution may be to simply take more kratom if digestion is poor. While this may work, it also increases the risk of side effects like nausea or vomiting (and potentially worsen digestive health further).
People with poor digestive health should make it a point to strengthen their digestive health — if only for the purpose of increasing the effectiveness of their painkillers.
Many people with poor digestive health find that mixing some ginger tea or ginger powder with their kratom will significantly shorten the onset time and improve the potency of their kratom. Ginger increases blood flow to the gut and stimulates the release of liver and pancreatic enzymes that help nutrients break down and absorb.
Kratom extract tablets are also a good option because these products require far less work for the gut to process them.

C) Onset Time Is Affected by Product Type
Some forms of kratom kick in much faster than others.
The fastest onset comes from tinctures. Tinctures can be held under the tongue to enable sublingual absorption (absorption through tiny blood vessels on the bottom of the mouth). This method allows the active ingredients to enter the bloodstream in as little as 10 minutes.
Consuming the raw powder using the “toss ‘n’ wash” method is also pretty quick to kick in. This method inevitably results in some sublingual absorption, as well as rapid absorption through the stomach and small intestines. Most people report the onset of effects begins around 15 minutes after taking it, with the full effects reached by the 45-minute mark.
Capsules can take a little longer because they don’t allow for sublingual absorption, and it can take some time for the gelatin capsule to break down in the stomach. Most people report the effects of capsules to take about 10–20 minutes longer than the raw powder.
How Long Does Kratom Last?
The effects of kratom last between 5 and 7 hours, but some lingering effects can remain for a total of about 12 hours.
Kratom will remain in the system in trace amounts for about 24 hours in total.
In general, if using kratom for pain, you’ll need to redose every 5 or 6 hours to provide consistent pain relief. But it’s important to remember that as the effects wear off, some kratom is still in the system. It’s wise to take smaller doses for maintenance dosing (second or third doses after the first dose of the day wears off).

Kratom For 11 Different Types of Pain
Kratom is one of the best natural painkillers on the planet. It targets pain through the opioid receptors, as well as ancillary mechanisms like blocking calcium channels, inhibiting neuromuscular junctions, blocking key inflammatory pathways, and even increasing tolerance to pain [34].
The way it should be used depends on the type of pain you’re experiencing.
Factors like chronic versus acute pain, the physical location of the pain, the root cause of the pain, and even what time of day the pain is at its peak are all factors to consider when deciding which type of kratom to use and how to apply it effectively.
Let’s examine the best way to approach kratom for different kinds of pain.
1. Kratom For Nerve Pain
Nerve pain (also called neuralgia or neuropathic pain) refers to pain that originates in the nerve cells directly. This kind of pain feels different from other types of pain and is one of the hardest forms to treat.
Nerve pain is usually caused by damage to the neurons. Diabetes, autoimmune disease, Parkinson’s disease, Huntington’s disease, strokes, and cancer can all cause damage to the neurons resulting in substantial amounts of pain.
A few examples of conditions characterized by nerve pain include trigeminal neuralgia, sciatica, and shingles virus (Varicella zoster).
Using kratom to manage nerve pain effectively involves taking higher doses of either a red or green vein kratom strain. Strains that contain higher concentrations of neuroprotective agents such as corynoxine A and B (such as Red Bali or Red Borneo) likely offer the best results for this kind of pain.
Corynoxine has been shown to provide direct neuroprotective effects. One study reported this compound helps to repair neuronal damage and neuropathic pain associated with Parkinson’s disease [3].
It’s common for users to combine kratom with other neuroprotective herbs, such as skullcap (Scutellaria lateriflora) and lion’s mane (Hericium erinaceus).

Nutritional supplements that support neuronal health can help in the long run, too (such as phosphatidylserine, alpha-GPC, or B vitamins). The goal is to provide as much support to the nervous system as possible so the damage can be fixed — thus eliminating the pain for good.
In most cases, users need to take fairly large doses of kratom to provide sufficient relief from neuralgia — but it depends entirely on the individual.
As always, start low, and increase the amount of kratom used with each consecutive dose until you find a dose that works well for you.
2. Kratom For Muscle Pain
The most common cause of muscle pain is overuse, injuries, and chronic tension.
Kratom is useful for managing muscle pain through two key effects — it blocks pain transmission via the opiate receptors, and it forces the muscles to relax.
The best strains to look at when addressing muscle pain are those that also contain higher levels of 7-hydroxymitragynine and a minor alkaloid called mitraphylline.
Mitraphylline is believed to be the primary muscle relaxant in the plant. Recent studies have shown that kratom reduces muscle tension by targeting the neuromuscular junctions that control them rather than at the site of the muscle directly [4]. This offers an additional layer of pain relief for muscle-specific pain or discomfort.
Strains that contain the highest levels of mitraphylline are typically those from either Borneo or Bali (Red Bali, Green Bali, or Red Borneo and Green Borneo Kratom).
Alongside kratom, other techniques should be used to offset the pain and facilitate faster recovery so you can eventually stop using kratom. This includes things like stretching and yoga, drinking plenty of water, visiting a physiotherapist or massage therapist, or taking other herbal and nutritional supplements to ease inflammation and promote faster muscle recovery.
Related: Kratom For Golf Injuries
3. Kratom For Joint Pain
Joint pain is a symptom, not a condition. The most common culprit of this condition is arthritis — of which there are several different types (rheumatoid arthritis, osteoarthritis, and psoriatic arthritis). Other causes of joint pain include conditions such as gout, fibromyalgia, bursitis, viral infection, and physical injuries.
Kratom helps to reduce joint pain through several mechanisms. It dulls pain transmissions by activating the opioid receptors and helps address the underlying cause by blocking inflammation inside the joints themselves.
In most cases, however, kratom can only offer symptomatic relief for joint pain. Identifying the underlying cause and hitting it directly with physiotherapy, nutritional supplements, and lifestyle changes are essential for longer-term relief.
The best kratom, overall, for joint pain are red vein strains that also contain rhynchophylline or epicatechins (great for managing low-grade inflammation associated with arthritis). These strains include Red Bentuangie, Red Indo, or Red Malay.
Green vein kratom strains like Green Bentuangie or Green Indo are also great options for people who find red strains a little too sedating.
People who suffer from osteoarthritis may find even greater benefits by combining their kratom with another herb called frankincense (Boswellia serrata). Frankincense supplements block a specific inflammatory mediator called 5-LOX that’s involved in the pathophysiology of osteoarthritis. This is a target that’s missing in kratom, so combining this herb is believed to synergize with the painkilling benefits for this particular condition.
For rheumatoid arthritis, it’s wise to combine kratom with immunomodulatory herbs like reishi (Ganoderma lucidum), turmeric (Curcuma longa), or ashwagandha (Withania somniferum) as well.

4. Kratom For Headaches
There is a multitude of potential causes of headaches. Our head contains the largest concentration of neurons in the entire body, so it’s easy to see how this part of the body could be especially susceptible to all kinds of pain.
Some of the most common causes of headaches include dehydration, side effects from other drugs or medications, allergies, cold/flu, stress, hangovers, poor posture, and problems with eyesight. Headaches can even form as a result of pain in other areas of the body, such as chronic back or joint pain.
Migraine headaches are a particularly severe form of headache pain. It can cause sufferers to become extra sensitive to light and sound, throbbing pain inside the head, loss of taste or smell, and extreme fatigue. They often come on suddenly with little warning.
Another type of headache, called cluster headaches, involves the sudden onset of severe pain around one side of the head or around one eye. They tend to come in waves (clusters) of significant pain, followed by periods of little to no pain.
Related: What’s the Difference Between Migraines & Cluster Headaches?
Kratom works best for minor headaches that aren’t caused by dehydration. Some users report kratom to be effective for cluster headaches as well, but fewer people find relief from migraines or dehydration headaches.
The problem with kratom for treating headaches is that it’s both a diuretic (makes users have to pee) and is emetic in higher doses (induces nausea). People who are dehydrated could become even more dehydrated, and people feeling nauseous during a migraine attack may become even more nauseous after taking kratom.

If using kratom to help manage a headache, it’s wise to start with a big glass of water first, followed by either a kratom tincture, kratom capsule, or kratom extract. Kratom powder can work well too, but its effectiveness is limited by its pungent, bitter taste and emetic nature.
Some people turn to kratom to help manage headaches from hangovers as well — but the same rules apply. The headache involved in hangovers is usually a combination of magnesium deficiency and dehydration, so the first course of action should be to restore these nutrients. Only after that should kratom be used to help reduce symptoms.
In all cases, kratom should be avoided if nausea is present.
5. Kratom For Back Pain
According to the Centers for Disease Control (CDC), back pain is the most common cause of pain (at least in the United States). Nearly 40% of the CDC’s study respondents reported back pain within the past 3 months.
It makes sense; the back requires a lot of dynamic movement, carries a lot of weight, and is especially susceptible to injury. Thirty-one pairs of spinal nerves travel through the inside of the spinal cord, which is protected by 33 individual, flexible vertebrae — damage to even one of these elements can result in serious pain.
The most common causes of back pain include injuries to the spinal cord or muscles, sciatica, ankylosing spondylitis, slipped discs, poor posture, or natural age-related degeneration.
Back pain can also present without any clear indication of damage or dysfunction (a form of psychosomatic or functional pain syndrome).
Kratom is an excellent go-to for chronic back pain for a few reasons:
- Kratom is preferred for long-term use over prescription opiates because it’s both less dangerous and less addictive.
- Kratom targets the opiate receptors to provide effective pain relief for even the most severe manifestations of pain.
- Kratom provides mild anti-inflammatory effects, which can help offset some of the pain and may help prevent premature degeneration of the vertebra.
- Kratom contains neuroprotective agents that may help to repair damaged neurons.
The best kratom strains for chronic back pain include potent red vein varieties like Red Bali Kratom or Red Maeng Da Kratom. Green vein strains such as Green Bali and Green Malay can also be useful and tend to be better for use during the day (less drowsiness as a side effect).
6. Kratom For Abdominal Pain
There are many potential causes for abdominal pain — some of which are serious and may require prompt medical treatment (such as appendicitis, ischemic bowel, or ectopic pregnancy).
Always seek the opinion of a medical professional if you experience severe, persistent, or sudden abdominal pain. In most cases, abdominal pain is caused by other, more benign conditions (such as constipation, irritable bowel syndrome, or food poisoning).
Kratom is a great all-purpose pain reliever, but it doesn’t work for all types of abdominal pain. While all forms of pain will be reduced by activation of the opiate receptors, some of the side effects of kratom could end up making symptoms even worse.
For example, kratom can cause nausea and vomiting (especially with higher doses). This can cause stomach or intestinal pain to worsen. Kratom can also cause constipation, which may further worsen digestive-related pain.
Other sources of pain, such as urinary tract infections, menstrual cramping, pulled muscles, broken ribs, kidney stones, and endometriosis, are likely to improve from using kratom.
Of course, the main goal of treatment should always be to identify the underlying cause of the pain and address this directly. Kratom is unlikely to treat the underlying cause of this type of pain.
In summary, kratom should only be used for symptomatic support of abdominal pain after visiting a doctor for an official diagnosis.
Kratom should be avoided if the underlying cause of pain originates in the digestive tract (the exception here may be stomach ulcers), the liver, the adrenals, or the kidneys.

7. Kratom For Psychosomatic (Nociplastic) Pain
Psychosomatic pain is a term used to describe pain that cannot be linked to any particular physical causes. It was believed this type of pain originates in the mind rather than the body, but this explanation is no longer accepted by most medical professionals.
Just because medical diagnostics may not be able to identify the specific source of pain doesn’t mean there isn’t a good explanation for what’s causing it.
Conditions that are often lumped into this group include fibromyalgia, trigeminal neuralgia, and interstitial cystitis — but there are many others. Basically, all forms of pain where a source can’t be accurately identified is considered psychosomatic.
There are many factors involved in the development of psychosomatic pain disorders, including:
- Anxiety & depression
- Childhood trauma
- Chronic or severe stress
- Genetic predispositions
- Individual pain tolerance (which can vary throughout life)
- Toxic exposure
- Viral infection (such as Epstein Barr or Herpes simplex)
Kratom may work for psychosomatic pain by alleviating several associated factors — including depression, anxiety, and increased pain sensitivity.
One study found that kratom significantly improved pain tolerance among study participants [8].
The specific type of kratom used in this study was not mentioned, but in general, the best kratom strains to use for fibromyalgia or other forms of psychosomatic pain depend on whether fatigue is also a significant factor for the individual.
If fatigue is a problem, it’s best to go for white vein kratom strains with stronger energizing effects — such as White Bali or White Papua.

If fatigue is less of an issue, red vein kratom strains, including Red Maeng Da, Red Bali, or Red Hulu, are likely going to offer more thorough pain relief for this particularly challenging form of pain.
Some people choose to use both — an energizing white vein in the morning and midday and a more relaxing red vein in the evening before bed.
8. Kratom For Cancer & Chemotherapy Pain
Pain is a common symptom among cancer patients. Both the condition itself, its diagnostic tests, and its treatment can all cause severe and persistent pain in different areas of the body.
Kratom may help alleviate much of the pain resulting from chemotherapy and certain types of cancer, but it will work better for some types of pain and may worsen others.
The different types of pain kratom is likely to support in relation to a cancer diagnosis includes:
- Joint pain
- Muscle pain and spasms
- Pain from lying in the same position for several days
- Peripheral neuropathy (nerve pain)
- Radiation-induced pain
- Sudden pain flares
- Vascular necrosis pain (pain caused by damaged blood vessels)
The types of pain kratom isn’t so useful for treating in relation to cancer includes:
- Burning and itching of the skin due to chemotherapy
- Ostealgia (bone pain)
In general, a strong green vein kratom is the most popular option for people with chemotherapy or cancer-induced pain. This is because green vein kratom also benefits the low energy levels associated with chemotherapy.
Strains such as Green Maeng Da, Green Malay, and Green Bali are the most popular.
But remember that everyone is different, and getting the right dose is critical. Take too much, and you’re going to make other chemotherapy symptoms like nausea or diarrhea even worse.
Start low, and go slow. Be patient and listen to your body.
Always ask your doctor before taking kratom if you’ve been diagnosed with cancer or are currently receiving treatment for cancer.

9. Kratom For Ischemic Pain
Ischemia refers to inadequate blood flow. When blood is unable to reach the cells due to blockages, the cells quickly begin to die from a lack of oxygen and nutrients. This cell death triggers a pain response to warn the body that something is very wrong.
Ischemia is serious and can quickly lead to death if not promptly treated. Heart attacks and strokes are both forms of ischemia. When blood is unable to enter the brain or feed the heart, it results in irreversible damage in as little as 20 minutes.
Milder forms of ischemia aren’t life-threatening but can cause long-lasting and hard-to-treat pain. Ischemic limb pain, for example, can develop as a result of other chronic health conditions like high cholesterol, diabetes, obesity, smoking, or high blood pressure.
Kratom can help with this kind of pain by dulling the pain signals sent from the limbs to the brain — but it won’t do anything to correct the underlying cause.
This kind of pain requires various treatments and lifestyle changes in order to be corrected. In many cases, ischemic limb pain is irreversible.
Some strains may be better for others in managing this kind of pain. For example, strains that contain high concentrations of the alkaloids corynanthine A, and corynanthine B are especially useful for this kind of pain by helping to reduce blood pressure in the affected arteries.
Strains with higher levels of corynanthine A and B include white vein strains like White Hulu Kratom.

10. Kratom For Withdrawal Pain
One of the best uses for kratom is to offset the pain and general discomfort involved with opiate withdrawal. It’s also been used to alleviate the pain, muscle spasms, insomnia, and malaise associated with the withdrawal of other chemicals, such as amphetamines withdrawal, opiate withdrawal, benzodiazepine withdrawal, and alcohol withdrawal.
Withdrawal symptoms develop when someone who is dependent on a drug stops taking it — or when the effects wear off between doses.
The withdrawal symptoms of a given drug usually present as the opposite of the drug’s normal effects.
The effects of opiates are to block pain, induce feelings of euphoria, and cause feelings of sedation and sleepiness.
Therefore, as the effects of the drug wear off and withdrawal symptoms appear, the usual symptoms are things like insomnia, increased sensitivity to pain, and depression.

Kratom is especially helpful for opiate withdrawal because it presses many of the same buttons as this class of drug. By activating the opiate receptors in an opiate-dependent individual, withdrawal symptoms can be reduced.
As such, kratom is commonly used as a sort of replacement therapy. Users slowly wean themselves off chemical opiates and on to kratom instead — which acts as a much milder opiate. Once the patient is using kratom instead of the drug, they can wean off kratom more easily.
11. Kratom For Postnatal Pain
Pregnancy causes a lot of changes in the body — some of these changes, including changes in posture, increased pressure on the lower back and pelvic floor, and muscle stretching and thickening of the ligaments around the abdomen can result in lasting pain for new mothers.
While kratom can certainly help alleviate post-natal pain, it’s wise to avoid the plant until after breastfeeding is complete. The active alkaloids inside kratom can pass into the breast milk, potentially causing harm to the developing child.
Kratom is not safe to use while pregnant or breastfeeding.
Only women who are not breastfeeding should consider using kratom to help manage post-natal pain.
Like other forms of pain, kratom works best if used in conjunction with other treatment options that address the underlying cause of the pain. Pelvic floor exercises and other forms of physiotherapy, exercise, yoga, and nutritional supplements like glucosamine, DHA/EPA, and a good multivitamin are all great options for women experiencing pain post-pregnancy.

How to Take Kratom For Pain
There are many ways to take kratom, each with its own set of pros and cons.
Most people use the raw powder, which is either consumed as-is, steeped in some hot water like tea, or encapsulated in gelatin or paper.
Kratom extract tablets are a newer but increasingly popular option as well for their improved flavor profile and pre-measured doses.
You can also find specialty products like kratom gummies or kratom shots that seek to improve the flavor and simplify the process of measuring out the right dose of kratom.
It’s unwise to smoke, vape, snort, or boof kratom for any reason.
Here are 5 popular methods of using kratom and tips for getting the most out of them to help with pain:
Toss ‘N’ Wash (Most Popular)
Kratom requires a relatively high dose to effectively manage pain, so most users rely on a tried and true method called the “toss ‘n’ wash method. This involves swallowing some raw kratom powder and washing it down with a big cup of water or juice as quickly as possible.
There’s no getting around it; kratom tastes awful. This method accepts this reality and gets it over with as quickly as possible — kind of like ripping off a bandaid. Fruit juices like mango or pineapple juice tend to do the best job of masking the taste, but anything will do.
Related: How to Use Kratom Powder

Capsules or Parachutes
The second most popular method is to use kratom capsules. This works great for avoiding the nasty taste of kratom powder, but because of the relatively high doses many people need to effectively manage pain, it can often involve taking several capsules at a time.
Parachuting kratom is another viable option. This method involves wrapping kratom powder in some cigarette paper and swallowing it like a capsule. It works in a pinch if you don’t have any capsules and want to avoid the kratom taste, but the paper can sometimes tear open in your mouth or throat, dumping the bitter contents out without expecting it. Parachutes also don’t avoid the issue with the dosage — so you’ll likely need to take several per day to get the desired effects.

Kratom Tea
A tea can be made by steeping kratom leaves or kratom powder in some hot water.
This method improves the taste (slightly), but it’s one of the least efficient ways of using the plant.
When you steep leaves in water, the active constituents need to diffuse from inside the leaf material into the water. This process can take a long time and will never provide 100% saturation. When you throw the leaves out after you’re done, you’ll be throwing away much of the active ingredients along with it.
When using kratom for managing pain, you’ll want to get as much out of the leaves as possible. The only way to do this is to consume them whole in the form of a powder.
Teas are generally preferred for people looking for the energizing or focus-enhancing effects of kratom (which benefit most using lower doses).

Kratom Extract Tablets
Kratom extracts have been around for a long time, but there were a lot of problems with them that made them unpopular (primarily adulteration).
Additionally, when you isolate individual compounds from plants, the effects they produce tend to differ from the effects of the whole plant.
With kratom, this issue is very pronounced.
We know that alkaloids like mitragynine and 7-hydroxymitragynine are responsible for the majority of the painkilling effects of the plant, but when you isolate them, the potency tends to go down rather than up. This suggests that many of the other alkaloids and phytochemicals in the plant are needed to “unlock” the painkilling power of these key ingredients.
A new form of extracts, called kratom extract tablets, seeks to solve this issue by providing increased concentrations of all the alkaloids present in the plant. Instead of isolating one alkaloid in particular, these extracts work by removing the non-essential components like plant fibers, fats, sugars, and proteins — leaving behind all the alkaloids (including, but not limited to, mitragynine and 7-hydroxymitragynine).
The result is a very strong product without the bitterness and grassy taste of the raw powder.

These kratom extract tablets are quickly becoming the go-to for people using kratom on a daily basis to relieve pain.
To use them, simply crush the tablet in a mug and pour boiling water over them. Add some juice or sugar to sweeten the mixture, and give it a good stir to ensure the tablet dissolves completely before drinking.
Kratom Tinctures
Liquid extracts and tinctures are the standard method traditional herbalists use to administer medicinal herbs.
Kratom tinctures are typically made by soaking the dried and powdered leaves in a solvent such as alcohol or glycerine. The active ingredients diffuse from the leaves into the liquid, which is then strained to remove any solid components.
The benefits of herbal tinctures include:
- Tinctures are easily combined with other herbal tinctures to create complex synergistic formulas
- Tinctures have a fast onset of effects (especially if allowed to absorb under the tongue before swallowing)
- Tinctures are preserved in alcohol, which gives them a very long shelf-life
- Tinctures make dosing simple by allowing users to count the drops or volume rather than weight
To use a kratom tincture, simply measure out the recommended dose listed on the bottle using the included dropper (or a small measuring cup). You can add the tincture to water or juice or take it straight up.
Keep in mind the potency of tinctures can vary depending on how it was made. Most kratom tinctures are either 1:1 (meaning 1 mL of tincture is equal to 1 gram of leaves), 1:2 (1 mL of tincture is equal to 0.5 grams of leaves), or 1:5 (1 mL of tincture is equal to 0.2 grams of leaves). Always follow the instructions on the label to avoid taking too much.

Where To Buy Kratom
You can find kratom abundantly online and in specialty shops around the world. Keeping in mind the metrics we’ll describe below, our recommended vendors for 2023 as Kona Kratom, Star Kratom, and VIP Kratom.
Learn more about how we vet kratom vendors.
There are 4 main issues with kratom to be aware of when selecting which vendor to order your kratom from:
Price Inflation
All kratom comes from farmers in Southeast Asia, especially around Indonesia and Bali. From the time kratom is harvested until the time, it shows up on your doorstep, it may have traded hands as many as 10 times.
There are a lot of middlemen in the world of kratom.
Every time kratom changes hands, a “tax” is imposed as each wholesaler and vendor takes their cut.
The quality of kratom tends to go down the more it’s passed around too.
Therefore, the best kratom vendors to buy from obtain their kratom directly from farmers or as close to the source as possible.
Contamination
Like many plants, when the air and soil are contaminated, kratom becomes contaminated too. Common contaminants within kratom are lead and other heavy metals (from soil contamination), pesticides, solvents, and microbial contamination (from improper storage).
There’s also a major issue with purposeful contamination (called adulteration). Unethical companies buy large amounts of low-grade kratom at a discount and try to boost its effects by adding synthetic chemicals.

Some of the adulterants reported in kratom products include phenethylamine (a stimulant) [10], excessive and unnatural levels of 7-hydroxymitragynine [15], and opiates such as morphine and hydrocodone [16].
For this reason, it’s wise to avoid any vendor that isn’t approved by the American Kratom Association (AKA) and provide clear evidence of third-party testing directly on their website.
Third-party testing is a practice where vendors send a sample of each kratom batch at their own cost. The third-party lab should have no affiliation with the vendor. These labs will scan the kratom for potential contaminants and assess the overall potency of the product.
Fake Kratom
Unregulated marketplaces are rife with scammers. Kratom is no exception.
It’s not uncommon for people to fall victim to scammers selling fake kratom. They build a nice website and position their product to look like high-quality kratom at bargain prices. Some of these scams will ship you a product that either contains very low-quality (and often adulterated) kratom powder or something entirely different (such as the ground-up leaves mixed with other chemicals).
In other cases, the scammers will simply steal your money and send you nothing in exchange.

Unethical Farming Practices
The kratom industry has the unique ability to both protect or destroy the natural habitat it comes from.
Traditional farming practices involve planting kratom within its natural habitat. This practice not only protects the critical rainforests of Southeast Asia, they directly improve them. These trees are often picked by hand and fertilized by the forest itself.
Of course, ethical farming is less lucrative than clearcut monocropping methods. These modern farms are created by clearing vast areas of tropical rainforest and replacing them with perfectly optimized geometric rows of kratom clones. They’re harvested using machines rather than by hand, and they’re fertilized using aggressive chemical fertilizers and sprayed with pesticides that seep into the local rivers and lakes, killing the fish, reptiles, and amphibians that live there.
It’s important to support companies that source kratom from farms that improve the integrity of these critical rainforests rather than those that accelerate their destruction.

Is Kratom Safe To Use As A Pain Reliever?
Kratom is an excellent pain reliever and offers clear advantages over conventional painkillers — but it isn’t without its risks.
Any compound, natural or synthetic, that has a biological effect on the body carries the risk of side effects.
Kratom has a particularly strong effect on the body, so with it comes a higher risk of side effects than less medically valuable herbs like mint, turmeric, or ginger.
So what, exactly, are the risks of kratom? How dangerous is it, and how can you avoid them?
Overall, kratom is very safe. Kratom will not kill you, but you might feel sick for a few hours if you take too much. Its side effects are a reflection of its therapeutic effects.
There’s a famous quote by Pliny the Elder that sums this up quite well:
“The difference between poison and medicine is in the dose.”
Like all therapeutic herbs, the dose is key. You want to take enough kratom to enjoy its benefits without going far enough to suffer its side effects.
The characteristic sign you’ve taken too much kratom is a collection of symptoms called the “kratom wobbles.”
Kratom wobble consists of feelings of nausea, dizziness, and reduced muscle coordination. As users walk, they both look and feel like they’re wobbling all over the place.
This is not a place you want to end up, but it’s not particularly dangerous either — it’s just very uncomfortable.
The best thing to do if you experience side effects from kratom is to find a spot to lie down, drink some water, and try to sleep it off.
Kratom can also produce feelings of anxiety (caused by its beneficial energizing effects), it can make you feel drowsy and sedated (caused by its calming effects), dizzy (caused by its euphoric effects), or anxious (caused by its energizing effect).
Side Effects of Kratom May Include:
- Anxiety or restlessness
- Constipation
- Diarrhea
- Dizziness
- Depression
- Frequent urination
- Headaches
- Heart palpitations
- High blood pressure
- Low libido
- Nausea and vomiting
- Numbness
- Sedation and prolonged sleepiness
Learn more about the side effects of kratom and how to avoid them.
Is Kratom Addictive?
Yes, kratom can be addictive if abused or taken without breaks.
Any substance — herbal or pharmaceutical — that offers some form of relief for the body (in this case, elimination or reduction in pain) can be used as a crutch. When pharmacologically active substances are used over and over, the body starts to resist their effects — eventually leading to dependence.
Dependence means the body relies on the presence of a certain substance to maintain homeostasis (balance). When the substance is removed, balance is lost, resulting in a group of side effects known collectively as “withdrawal.”
Kratom can be addictive if used for long periods of time without a break. This quality is a byproduct of its inherent health benefits. No substance that offers the level of relief kratom can be expected to avoid the risk of compulsive use.

Perhaps the saving grace for kratom in terms of its addictive potential is the fact that it doesn’t contain just one active ingredient — it contains several. Each compound targets different receptors, which helps slow the formation of tolerance.
By comparison, synthetic opiates like oxycodone, morphine, and heroin are highly selective to the mu-opiate receptors. It doesn’t take much time for the body to begin resisting the effects of these drugs — leading to dependence and addiction.
You know you’re addicted if you find yourself using the herb compulsively despite it having a clear negative impact on your health, social relationships, or other areas of your life.
Kratom is a tool to help users get through rough patches of acute or chronic pain. It should never be used as a permanent crutch.
Those who abuse the herb — either by taking large doses in order to get high or taking it without addressing the underlying cause of the pain — carry the highest risk of becoming addicted.
How to Avoid Addiction to Kratom
The best way to avoid becoming dependent on kratom is to take periodic breaks and to be honest with yourself about your relationship with the plant.
Even with long-term use, it’s wise to take a week off or significantly reduce the dose of the herb for a week every month or so. This simple practice has helped millions of users avoid full-fledged addiction despite taking it for several months or even years at a time.
Kratom should always be used in conjunction with other therapies aimed at eliminating the underlying source of the pain. The ultimate goal is to eventually stop using kratom.
For those who can’t (due to chronic health conditions), steps should be taken early to offset the potential for physical dependence on the herb.
Luckily, physical dependence on kratom takes a long time. The amount of time it takes depends on the dose, the frequency of use, and various other genetic and social factors. Most people can take the herb for years without becoming addicted.

What Are the Side Effects of Kratom Withdrawal
Withdrawal symptoms always present as the opposite effects of the substance being used.
The effects of kratom are to increase energy, block pain, improve mood, and relax the muscles.
Therefore, kratom withdrawal symptoms tend to include fatigue and lethargy, depression, increased sensitivity to pain, and muscle tension.
Other symptoms include runny nose, constipation, agitation and insomnia, mood swings, and headaches.
Cravings to use kratom are another key side effect. The body intuitively knows that the only way to eliminate these uncomfortable side effects in the short term is to take more kratom.
But just as the body develops tolerance over time, it will reverse it naturally with time as well. This can only happen if kratom is avoided or weaned off gradually.
For most people, the withdrawal symptoms of kratom are pretty mild. Users feel tired and worn out for a few days after ceasing. They may experience a headache for the first day or two and will likely experience a strong desire to use more of the herb. Digestive discomfort and insomnia are also common — especially in the first couple of days. In most cases, symptoms are gone within two weeks.
Related: How to Quit Kratom
Will Kratom Damage the Liver?
Kratom is unlikely to cause liver damage but should be avoided if using hepatotoxic medications or in conjunction with liver disease.
If you experience yellowing of the skin or conjunctiva of the eyes or notice brown or red discoloration of the urine — stop taking kratom immediately and visit your doctor.
Kratom and its many alkaloids are processed in the liver. Special enzymes located in the liver cells systematically break down and deactivate alkaloids like mitragynine and 7-hydroxymitragynine to prepare them for filtration through the kidneys.
When kratom is taken alongside drugs or medications known to cause damage to these enzymes or used in combination with preexisting liver disease, it can speed up the degenerative process.

Safety Comparison of Kratom vs. Opiate Drugs
Many people turn to kratom as an alternative to opiate-based prescription painkillers (as well as illicit opiates) because it offers comparable painkilling action without the risk of fatal overdose.
Kratom is also significantly less addictive than its pharmaceutical counterparts because it’s less specific to the mu-opioid receptors, less potent overall, doesn’t inhibit beta-arrestin-2, and is more difficult to abuse (can’t be effectively injected, snorted, or smoked).
Kratom lacks two of the major components that make synthetic opiates so dangerous:
Kratom Causes Users to Vomit Well Before Reaching Toxic Levels
It’s very difficult to overdose on kratom because it causes users to feel nauseous and throw up long before it has a chance to reach toxic levels. This ejects kratom from the digestive tract and prevents any further absorption. This effect is very uncomfortable — it’s hard to imagine someone taking more kratom once they start feeling these effects.

Kratom Doesn’t Affect the Respiration Rate
Kratom also lacks the inhibitory action on beta-arrestin-2 [6, 7] — which controls our respiration rate.
Inhibition of this receptor is the leading cause of death by opiate drugs like heroin and fentanyl. If you take too much of these substances, it causes you to pass out and stop breathing.
Kratom does not do this.
Key Differences: Kratom vs. Prescription Pain Meds
| Comparison Metrics | 🍃 Kratom | 💊 Prescription Opiates |
| Effects On Pain | Moderate to strong pain-relief | Strong pain-relief |
| Overdose Potential | Very low risk of causing fatal overdose | High risk of causing fatal overdose |
| Impact on beta-arrestin-2 | No impact | Strong inhibition (leading to respiratory arrest in the event of overdose) |
| Potential for Addiction | Mild to moderate | Moderate to high potential for addiction |
| Mechanism of action | • Mu, delta, & kappa-opioid receptor agonism • Dopaminergic & serotonergic effects • NMDA agonist • GABAergic effects • Adrenergic receptor agonist | • Mu-opioid receptor agonist |
| Requires Prescription? | No | Yes |
Will Kratom Interact With My Other Pain Medications?
Any herb with a strong effect profile or that is metabolized via the liver is going to carry some risk of negative interaction with other drugs. This is not something unique to kratom.
Kratom is notoriously strong. This means there’s a higher risk involved with combining it with drugs that have similar actions or that block the body’s ability to metabolize it. The riskiest interactions involve anything in the opiate class, benzodiazepines, amphetamines (and other stimulants), and alcohol (or alcohol-like drugs such as GHB).
It’s important to consult your doctor before using kratom for any reason if you’ve been prescribed medications or have been diagnosed with a medical condition.
Opiate Painkillers
Kratom should never be used in conjunction with opiate painkillers. The only exception is the application of kratom replacement therapy for patients addicted to synthetic opiates. This should always be done under strict medical observation.
Opiate drugs carry a high risk of overdose and death. Mixing them with kratom could dramatically increase the potency of these drugs, resulting in fatal respiratory arrest.
List of Opiate Painkillers:
- Buprenorphine (Cizdol & Brixadi)
- Codeine
- Diamorphine (Heroin)
- Pethidine (Meperidine & Demerol)
- Fentanyl (Abstral & Actiq)
- Hydrocodone (Hysingla ER, Zohydro ER & Hycodan)
- Hydrocodone & Paracetamol (Vicodin)
- Hydromorphone (Dilaudid)
- Methadone (Methadose & Dolophine)
- Morphine (Kadian & Roxanol)
- Oxycodone (Percodan, Endodan, Roxiprin, Percocet, Endocet, Roxicet & OxyContin)
- Tramadol (Ultram, Ryzolt & ConZip)

NSAID Painkillers
Non-steroidal anti-inflammatory drugs (NSAIDs) such as Aspirin and Tylenol work by blocking a key inflammatory mediator known as COX-2. This enzyme converts arachidonic acid to proinflammatory cytokines that perpetuate the inflammatory cycle. By blocking this key enzyme, NSAIDs exert a powerful painkilling action without nearly the same compromise on safety as opiate medications.
One of the main alkaloids in kratom, mitragynine, has been found to offer similar COX-2 inhibition in vitro [12, 13].
While chances of negative interaction are slim, it’s wise to avoid mixing NSAID medications if you’re using kratom too.
These drugs are known to cause increased stress on the liver in normal doses and can cause irreversible damage in higher doses. While it’s unclear whether kratom actually increases the risk of liver damage from NSAIDs, until we can prove it doesn’t, this combination should be avoided.
List of NSAID Painkillers:
- Aspirin (Ascriptin, Aspergum, Entercote)
- Acetaminophen (Tylenol)
- Ibuprofen (Motrin, Advil, Nuprin, Caldolor & Neoprofen)
- Celecoxib (Celebrex & Onsenal)
- Naproxen (Aleve)
- Ketorolac (Toradol)
- Etodolac (Ultradol)
- Meloxicam (Mobic)

Benzodiazepine Muscle-Relaxants
Taking benzodiazepines and kratom should be avoided unless under explicit guidance from a medical professional. There is a safe way to mix these two drugs — but it involves strict discipline in terms of dosage.
Abuse of either Kratom, benzodiazepines, or both dramatically increase risk.
This combo increases the potential for side effects from both drugs, some of which are particularly problematic.
Kratom is emetic (causes nausea and vomiting) in high doses. Benzodiazepines are sedative. This is a terrible combination. Vomiting while unconscious can easily lead to death by suffocation.
List of Benzodiazepine Muscle-Relaxants:
- Alprazolam (Xanax)
- Chlordiazepoxide (Librium)
- Clonazepam (Klonopin)
- Clorazepate (Tranxene)
- Diazepam (Valium)
- Estazolam (Prosom)
- Flurazepam (Dalmane)
- Lorazepam (Ativan)
- Midazolam (Versed)
- Oxazepam (Serax)
- Temazepam (Restoril)
- Triazolam (Halcion)
- Quazepam (Doral)

Kratom For Pain: Research & Clinical Trials
The vast majority involving kratom focuses on its capacity for managing pain. There’s also research on the effects of kratom for treating anxiety and mood disorders, but neither of these applications hold a candle to the interest generated by kratom’s impressive painkilling action.
7-hydroxymitragynine and the closely-related mitragynine account for as much as 68% of the entire alkaloid content of the plant [26].
To no surprise, most research on kratom focus on either mitragynine or 7-hydroxymitragynine as the primary painkilling ingredients in the plant [5] — but in reality, kratom owes its powerful painkilling action to the combined effects of more than 16 active ingredients.
Here’s what some of the research says on the role each ingredient likely plays in controlling pain:
| Kratom Constituent | Main Effect | Overall Impact on Pain |
| 7-Hydroxymitragynine | Opioid agonist | 5 |
| Mitragynine | Opioid agonist α1 adrenergic agonist | 4.5 |
| Rhynchophylline | Calcium channel blocker NMDA antagonist | 2 |
| Ajmalicine | α1 adrenergic agonist | 2 |
| Corynantheidine | Opioid agonist | 2 |
| 9-Hydroxycorynantheidine | Partial opioid agonist α1 adrenergic agonist | 3 |
| Corynanthine | Adrenergic antagonist | 1 |
| Corynoxine A & B | Neuroprotective (improves autophagy) | 1 |
| Isopteropodine | Modulates muscarinic M1 receptors Modulates 5HT2A receptors | 3 |
| Mitraphylline | Increases cellular cAMP | 3 |
| Epicatechin | AntioxidantAnti-inflammatory Mild mu-opioid | 3 |
| Specioliliantine | Mild opioid agonist Mild serotonergic Anti-inflammatory α1 adrenergic agonist | 1.5 |
1. 7-Hydroxymitragynine
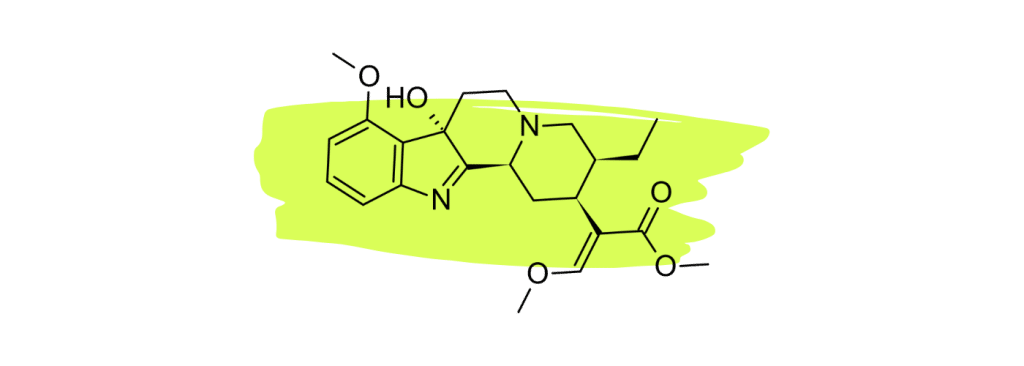
7-hydroxymitragynine (7HMG) is widely considered the strongest painkiller in the kratom plant. Numerous studies have shown this compound to be a powerful opioid agonist comparable to morphine [22 – 25].
The high concentration of this alkaloid in red vein kratom is what makes this particular strain type so effective for managing pain.
2. Mitragynine
Mitragynine (MG) is the second strongest (and most abundant) painkiller in kratom — working to block pain transmission before it reaches the brain (through opioid receptors) [18] and modulating the perception and sensitivity to pain within the brain through adrenergic (α1, α2), dopaminergic (D2), adenosine (A2A), and serotonergic (5-HT2A, 5-HT2C, 5-HT7) mechanisms [19 – 21].
Mitragynine has also been shown to inhibit the key inflammatory mediator COX-2 and prostaglandin E2 [32] and significantly reduces neuropathic pain in animal models [18].
3. Rhynchophylline
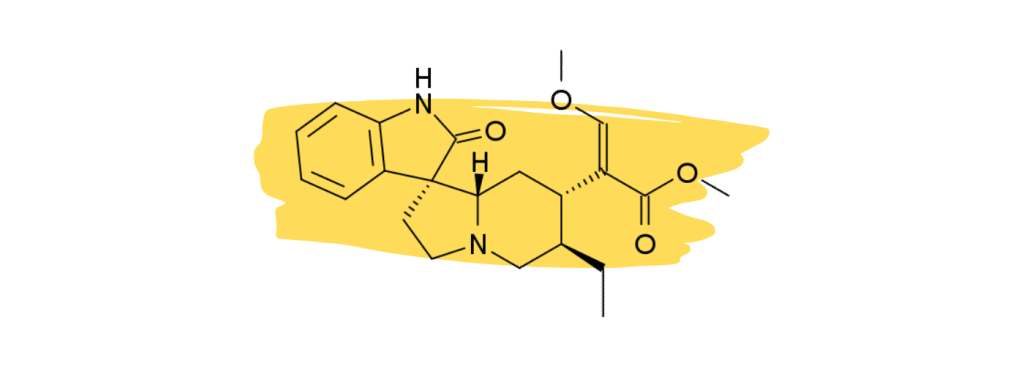
Rhynchophylline is a minor alkaloid in kratom that plays a supplementary role in the management of chronic inflammatory pain and vascular pain. It’s one of the primary active ingredients in another medicinal herb called Chinese Cat’s Claw which is used as a heart tonic and for treating neuropathic pain.
Studies have shown that rhynchophylline acts as a calcium channel blocker [26] — which is believed to reduce pain signals as they travel down the nerve axons.
Other studies have found that rhynchophylline acts as an NMDA antagonist [27]. NMDA receptors are heavily involved with neurotransmission. NMDA antagonists like ketamine and nitrous oxide are commonly used for anesthesia.
None of these effects are strong enough in kratom to provide painkilling benefits on their own but may instead act synergistically with the key analgesic agents 7HMG and MG.
4. Ajmalicine
Ajmalicine is not believed to offer direct painkilling action but may offer support for pain characterized by or aggravated by muscle tension.
This compound (also known as δ-yohimbine & raubasine) was shown to block the α1 adrenergic receptors [28]. One of the primary results of this action is the relaxation of skeletal muscle fibers.
5. Corynantheidine
Corynantheidine was shown to act in a similar manner to 7-hydroxymitragynine by activating the mu-opioid receptors [24,30].
This compound is a strong agonist of this key pain-regulating receptor, but the low concentrations of this compound only allow it to exert a mild analgesic action in practice.
6. 9-Hydroxycorynantheidine
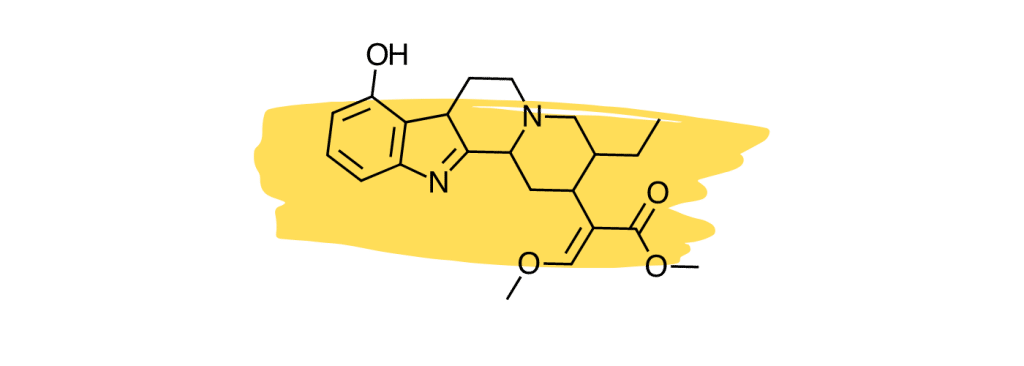
9-Hydroxycorynantheidine is structurally similar to yohimbine, a compound found in the bark of the yohimbe tree (Pausinystalia yohimbe) and is used as a stimulant and aphrodisiac.
This compound acts as a partial agonist to the mu-opioid receptors [29], which means it likely exerts similar painkilling effects as mitragynine or 7-hydroxymitragynine (full agonists), but to a lesser degree.
9-Hydroxycorynantheidine was also shown to activate the adrenergic receptors [30]. This action would likely work to improve feelings of fatigue and lethargy produced by other painkilling alkaloids like mitragynine and 7-hydroxymitragynine.
9-hydroxycorynantheidine is also believed to enhance the effects of other active alkaloids and slow their breakdown via the liver (thus making their effects last longer).
7. Corynanthine
Unlike most other kratom alkaloids, corynanthine has an antagonistic effect on the adrenergic receptors [31]. This effect contributes to the hypotensive effects of certain kratom strains. This effect may also help combat some of the side effects of other kratom alkaloids that target the adrenergic receptors (such as jitteriness, muscle tension, and rapid heartbeat).
This alkaloid is unlikely to directly contribute to the painkilling action of kratom but may help reduce the side effects of higher doses of the leaf.
8. Corynoxine A & B
Corynoxine A & B are also found in another medicinal herb called Uncaria rhynchophylla, which is a popular herb used in traditional Chinese medicine. This alkaloid has been studied for its neuroprotective and anti-inflammatory effects — for which it’s shown promising results.
One study found that corynoxine acted as an inducer for cellular autophagy [33] — which is a process by which the body actively destroys cells that have become damaged or dysfunctional. This process is a key element of homeostasis.
More specifically, this study found corynoxine to regulate autophagy through the Akt/mTOR pathway, which is involved in everything from metabolism to cellular proliferation. Researchers in the study suggest this gives corynoxine a neuroprotective action.
The effects of this alkaloid could be involved in the treatment of nerve damage and the resulting downstream impact this has on chronic pain.
9. Isopteropodine
Isopteropodine is also found in a plant called Isodon rubescens, which is a popular herb in traditional Chinese medicine for treating infections, cancers, and joint pain. It’s also found in the Amazonian herb Uncaria tomentosa (Cat’s Claw), where it’s used for similar applications.
One study found this compound modulated the function of both the muscarinic M1 and 5-HT2 (serotonin) receptors [35].
Activation of muscarinic M1 receptors has been shown to inhibit pain transmission in the spinal cord, possibly by modulating the release of neurotransmitters such as acetylcholine, norepinephrine, and dopamine. In addition, muscarinic M1 receptors have been shown to be expressed on sensory neurons in the periphery [36], where they may play a role in the transmission of nociceptive (painful) signals to the central nervous system. There is some evidence that muscarinic M1 receptor agonists may have potential as analgesic (pain-relieving) agents.
Activation of 5-HT2A receptors has been shown to inhibit the transmission of pain signals in the spinal cord and to modulate the release of pain-relieving neurotransmitters, such as endorphins and enkephalins [37]. There are several 5HT2A receptor agonists are currently being explored as potential analgesic agents — but so far, the results of this research are inconclusive.
10. Mitraphylline
Mitraphylline has been shown in several studies to possess anti-inflammatory and hypotensive effects. This alkaloid is primarily studied for its presence in the South American herb Uncaria tomentosa (Cat’s Claw).
This alkaloid works by modulating a molecule found in immune cells called lipopolysaccharide (LPS), which is tasked with breaking down cAMP (cyclic adenosine monophosphate) [38]. Other reports suggest mitraphylline also inhibits an enzyme known as phosphodiesterase (PDE) — which is responsible for breaking down cAMP.
This is important because these effects lead to an accumulation of cAMP in the cells. One of the downstream effects of elevated cAMP levels is a reduction in the transmission of pain signals — likely through the modulation of acetylcholine and GABA.
cAMP also activates the cAMP-dependant protein kinases (PKA) that modulate the function of various proteins involved in pain transmission.
Mitraphylline’s impact on cAMP is also involved in its anti-inflammatory action. One study found that animals administered mitraphylline experienced a reduction in various key inflammatory messengers — including a 50% reduction in TNF-α, a 70% reduction in IL-1ɑ and IL-1β [39], a 40% reduction in IL-4, and a 50% reduction in IL-17 [40].
Inflammation remains a key target for the management of chronic and acute pain of all forms.
11. Epicatechin
Epicatechin is a type of flavonoid found in a variety of plants, including coffee, green tea, cocoa, and various fruits.
This compound has an impressive antioxidant effect profile, protects the neurological system from damage, reduces inflammation, and improves cardiovascular health [41].
One study found that epicatechin also exerted notable pain relief on its own [42]. This study tested the effects of epicatechin alongside various receptor-blocking agents to determine the mechanism of action. Researchers discovered that epicatechin blocks pain via multiple receptors, including the 5HT (serotonin) receptors, mu-opioid receptors, and NO-cyclic GMP-K+ channels.
12. Speciociliatine
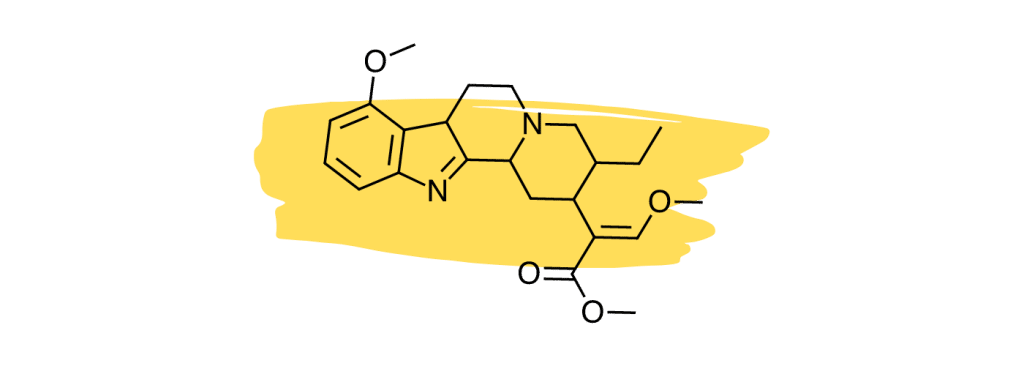
Studies suggest the minor kratom alkaloid, speciociliatine, is the second strongest-acting alkaloid at the mu-opioid receptors [30], which is considered the primary painkilling mechanism of the plant.
Despite the potency of speciociliatine at the opioid receptors, this alkaloid has little impact on the painkilling potential of the plant due to its low relative concentration. Future kratom strains may be developed that contain a higher speciociliatine content to leverage the effects of this useful alkaloid.
Speciociliatine also has a high affinity for adrenergic receptors similar to mitragynine and corynantheidine [30]. Its action is stronger at the α1 receptors than at α2.
III. Other Pain Therapies
Choosing the right therapy for pain management depends on various factors, including the type and severity of pain, the underlying cause, and what products or services you have access to.
Some people prefer natural pain therapies — such as other herbs like turmeric, boswellia, or blue lotus flower — others may prefer physical therapies like platelet-rich plasma, massage therapy, hot/cold therapy, or acupuncture.
Even certain philosophical practices, such as stoicism, can be helpful tools for managing persistent pain.
Regardless of which options you decide to try, the best way to deal with pain is to treat it at the source and to try several different tactics at once.
Here, we’ll explore some of the most popular and evidence-based pain therapies available today. There’s something here for all types of pain and all budgets.
11 Natural Pain-Relief Options
Humans have been tip-toeing around pain since forever. Pain is part of our existence and something we spend our entire lives trying to avoid as much as possible.
Pharmaceutical painkillers have only been around for about 200 years, but there’s evidence to suggest the opium poppy has been used since at least 3400 BCE. The use of other species of plants likely stretches back even further.
Humans from all over the world have tried and tested virtually every plant and fungi imaginable against pain.
Here are some of the best natural painkillers that have withstood the test of time (minus kratom, of course, the king of pain-relieving herbs).
1. Turmeric
Turmeric (Curcuma longa) has a long history of use in China and India. It’s considered a key Ayurvedic herb for managing the imbalances of all three doshas (Vada, Kapha, and Pitta).
Turmerics’ exceptional medicinal value comes down to its ability to manage inflammation — which is a key driver of pain and other chronic health conditions.
The active ingredient in turmeric, curcumin, acts as a potent COX-2 inhibitor and antioxidant [14] — offering the most relief for pain involving inflammation (such as arthritis, inflammatory bowel disease, and autoimmunity).

2. Boswellia
Frankincense (Boswellia serrata) is one of the strongest but least well-known herbal painkillers available. This plant is primarily used as an incense — its sticky resin releases a plume of aromatic terpenes when burned.
These terpenes are also powerful anti-inflammatory agents that work by blocking the effects of a unique proinflammatory regulator called 5LOX [43]. This effect works best for low-grade inflammation, such as osteoarthritis or chronic back pain. It’s also highly synergistic with COX-2 inhibitors like turmeric.
Other studies have found that boswellia mixed with myrrh (Commiphora myrrha) was able to significantly reduce neuropathic pain by blocking the TRP ion channels (TRPV1) [44].

3. Ginger
Ginger (Zingiber officinale) has been used as a natural pain remedy for thousands of years. When applied to the skin, ginger exerts a rubefacient effect. This effect increases blood flow to the area and exerts a hormetic action on inflammation (promoting inflammation in the short term to result in a net reduction in inflammatory status later). It’s useful in the form of topical creams and salves for treating arthritis and muscle pain.
When used internally, ginger acts as both a COX and LOX inhibitor, as well as an antioxidant and TRP ion channel antagonist [45] — helping to block inflammation and reduce pain.

4. Devil’s Claw
Devil’s claw (Harpagophytum procumbens) is a medicinal herb from Southern Africa used to manage various pain forms.
The active ingredients are a series of iridoid glycosides, which are most abundant in the roots and stems. These compounds have been shown to work best for chronic inflammatory conditions rather than acute inflammation [46]. This means devil’s claw may be a great option for people with long-lasting pain and inflammation, such as arthritis, chronic back pain, or autoimmune-related pain.
In a recent meta-analysis of clinical trials consisting of more than 6800 patients suffering from chronic low back pain or osteoarthritis, researchers reported just 3% of patients taking devil’s claw long-term experienced adverse effects — all of which were mild [47].

5. Ashwagandha
Ashwagandha (Withania somnifera) is primarily used as an adrenal tonic in traditional Ayurvedic medicine. However, its ability to regulate the hypothalamic-pituitary-adrenal (HPA) axis also makes it useful for certain kinds of pain — especially psychosomatic pain.
The active ingredient, withaferin A, was shown to alleviate neuropathic (nerve) pain in rats [48]. Ashwagandha works best with repetitive use. In this study, the rats were given doses of withaferin A for 15 days.

6. Cannabis (THC & CBD)
Cannabis (Cannabis sativa) includes both the marijuana plant and the hemp plant. Both are widely used for managing different forms of pain.
Hemp is defined as any Cannabis sativa plant that naturally contains no more than 0.3% tetrahydrocannabinol (THC). These plants produce much higher concentrations of cannabidiol (CBD) — which is non-psychoactive and widely regarded as the plants’ strongest painkiller. It works by regulating a system called the endocannabinoid system (ECS) — which itself acts as a regulator for inflammation, nerve function and repair, hormones, and post-workout recovery. It’s also been shown to interact with serotonin receptors (5HT1a), TRP ion channels (TRPV1), adrenergic receptors, adenosine [49], and COX-2 [50].
Marijuana refers to any Cannabis sativa plants that contain more than 0.3% THC by dried weight. These plants produce higher levels of THC or other cannabinoids, such as cannabichromene (CBC), cannabinol (CBN), cannabigerol (CBG), and more.
CBD and THC together appear to offer the most effective pain relief. A 50/50 combination of CBD and THC was found in numerous clinical trials to be effective in the treatment of rheumatoid arthritis pain [51], multiple sclerosis pain [52], chemotherapy and cancer-related pain [53], nerve pain [54], and more.
Learn More: What’s the Difference Between Kratom & CBD?

7. Moringa
Moringa (Moringa oleifera) is a tree native to India known for its nutrient-rich leaves, which are often used in traditional medicine and as a natural source of nutrients. Moringa is commonly known as the “miracle tree” or the “tree of life” due to its many potential health benefits — just one of which includes chronic pain.
The primary painkilling ingredient in moringa is a compound called moringin, which has been shown to activate the pain receptor channel TRPA1 (in vitro) [55].
Several of the herbal painkillers we’ve covered so far leverage the TRP channels as a way of reducing pain — including cannabis, boswellia, ginger, and kratom.
Moringa is also rich in antioxidants and nutrients essential for a healthy immune response (including inflammatory recovery) and nerve function (thus providing some support for neuropathic pain).

8. Blue Lotus Flower
The blue lotus flower (Nymphaea caerulea) resin was used ceremonially in parts of Northern Africa due to its sedative and oneirogenic (dream-inducing) effects. It owes these effects to a series of opiate-like compounds, including aporphine and nuciferine.
Despite structural similarities, neither aporphine nor nuciferine are strong opiate agonists. These compounds help alleviate pain in other ways, however.
Aporphine derivatives, for example, have been shown to act as dopamine (D1) receptor antagonists [56]. This mechanism is especially useful for combating neuropathic pain.
Nuciferine was also shown to inhibit COX-2 and a variety of cytokines involved with pain and inflammation (IL-6, TNF-α, and iNOS) [57].

9. Feverfew
Feverfew (Tanacetum parthenium) is used as a treatment and prophylactic for migraine headaches. It’s also traditionally used for managing arthritis pain and various forms of inflammation.
A group of compounds contained in feverfew called parthenolides work to alleviate or prevent migraine attacks through three distinct mechanisms:
- Inhibits serotonin release from platelet triggers [58]
- Inhibits the inflammatory molecule NF-kB [59]
- Reduces vascular smooth muscle spasms [60]

Other Techniques To Consider For Pain Management
Effective pain management often requires a combination of different treatment approaches, as different types of pain may require different types of treatment.
This is known as a multimodal approach to pain management.
Herbs and supplements are just the start — physical therapies, diet and lifestyle changes, and social factors should also be employed for a more well-rounded and comprehensive pain-management strategy.
Hot & Cold Therapy
Hot and cold therapy, also known as thermotherapy and cryotherapy, is a type of treatment that involves the use of heat or cold to help alleviate pain and inflammation in the body.
These therapies can be used alone or in combination with each other, and they may be applied through a variety of methods, including heating pads, ice packs, and hot and cold compresses [61].
Heat should be applied to muscle pain or tension, while cold therapy works best for acute pain or inflammation.

Acupuncture
Acupuncture is a form of traditional Chinese medicine that involves the insertion of small needles into specific points on the body. The idea is to alleviate pain and various other health conditions by restoring the natural flow of Qi (pronounced “chee”) in the body.
In traditional Chinese medicine, Qi is essentially our “life force” — which flows through the body. Qi is believed to be the source of good health and well-being. When it becomes inhibited or blocked, it leads to dysfunction and pain.
There are several theories about how acupuncture may help to reduce pain.
One theory is that acupuncture stimulates the release of endogenous opiates, such as dynorphin, endorphin, and encephalin, which are a group of pain-relieving chemicals produced by the body [62].
Acupuncture may also help to improve circulation, which can help to speed up the healing process [63].
There is evidence to support the use of acupuncture for the management of certain types of pain, such as low back pain [64], neuropathic pain [65], and osteoarthritis [66].
Platelet-Rich Plasma (PRP)
PRP is a modern therapy that involves the removal of a sample of one’s blood, from which the platelets are then separated using a centrifuge. The platelet-rich plasma is then injected into target areas of the body to stimulate healing and tissue repair. This therapy is typically used to treat pain from injuries to the musculoskeletal system.
PRP is thought to work to alleviate pain by promoting the release of growth factors and various other factors that stimulate the healing process [67].
Diet & Lifestyle
There are many factors in life that can lead to or exacerbate pain. The best way to manage chronic pain conditions is to first learn how to identify the factors causing or aggravating the pain and treat them at the source.
Diets high in refined carbohydrates and free radicals can promote inflammation underlying chronic conditions. Eat foods that are high in antioxidants and essential nutrients to give your body the best chance at recovery possible.
Lack of exercise or overexercise is also common causes of chronic pain. One study found that teenage boys with the lowest physical activity levels had a higher prevalence of pain [68]. Another study reported that long durations of sitting, specifically, carried the highest risk of chronic lower back pain [69].

Philosophy
Stoicism is an ancient Greek philosophy centered on the idea that through disciplined thought, we can live in accordance with reason and virtue.
Stoicism is a philosophy that addresses all matters of what it means to exist as a human, but it stands above the rest in the way it addresses pain and discomfort.
The stoics believed that pain and suffering are inevitable parts of life. Rather than allowing this discomfort to weigh them down, it was leveraged as a tool to better themselves and turn it into a source of strength rather than a source of weakness.
Here are some of the ways stoicism can help us deal with pain:
- Acceptance — Accept that pain is a natural part of life and try to focus on things that are within your control rather than dwelling on things that are beyond your control.
- Perspective — Try to maintain a larger perspective and keep things in perspective. Remember that pain is temporary and that it will eventually pass.
- Virtue — Cultivate virtues such as courage, justice, and wisdom, which can help you deal with pain and suffering in a more positive way.

Pain FAQs
We’ve covered a lot of information about pain already, but we’ve summarized many of our most commonly-asked questions below:
What is Pain?
Pain is both a physical and emotional sensation triggered by damage or potential damage to the body. It’s the body’s way of telling you about an injury and acts as a protective mechanism to prevent further harm.
What Are the Different Types of Pain?
Pain can be characterized in several different ways, but the most common are acute and chronic pain.
Acute pain is short-term pain that’s typically caused by some form of injury. This form of pain is usually resolved in a few days or weeks.
Chronic pain lasts much longer and is typically caused by conditions such as arthritis, cancer, nerve damage, or psychological factors.
What are the Most Common Causes of Pain?
Pain can be caused by a wide range of common factors, including traumatic injury, illness, medical conditions, menstrual cramps, muscle strains, or surgery.
How is Pain Treated?
The pain treatment depends on the severity and its underlying causes. Common pain treatments include using medications such as NSAIDs or opiates, as well as physical therapy, corticosteroids, or hot and cold therapy.
Can Pain Be Prevented?
In some cases, pain can be prevented. The best way to avoid pain is to protect the body from injury or illness. This may involve wearing protective clothing, practicing good posture, eating a well-balanced diet, avoiding tobacco or alcohol, and getting adequate exercise.

How Can I Manage Pain At Home?
There are a few ways to manage pain at home, but the best methods depend on both the severity of the pain and its cause.
- Apply heat or cold to the area — Heat is best for relaxing muscles and improving circulation, while cold is better for reducing inflammation and helps numb the area.
- Massage the affected area — Applying gentle massage may help improve circulation and speed recovery.
- Use over-the-counter medications — Nonsteroidal anti-inflammatory drugs (NSAIDs) may help reduce pain and inflammation.
- Take herbal supplements — Herbs like cannabis or kratom are excellent natural painkillers to take at home.
- Resting — Take a break from physical activity and prioritize a good night’s sleep to reduce inflammation and allow the body time to heal.
When Should I See a Doctor For Pain?
It’s important to visit a doctor if you’re experiencing severe or persistent pain.
If your pain is accompanied by fever, lightheadedness or confusion, and significant redness in the affected area, these could be signs of an infection and should be checked out by a doctor immediately.
Is it Normal to Experience Pain After Surgery?
Yes. It’s very common for people to experience pain following a surgical procedure. Many doctors will prescribe painkillers for the days following the surgery.
However, if you experience severe or persistent pain after the surgery, it’s important to contact your doctor.
Can Stress & Anxiety Cause Pain?
Yes. Stress and anxiety have been shown to contribute to the development of many chronic pain conditions — including headaches, back pain, and fibromyalgia. Stress may also further exacerbate existing pain conditions.
Psychosomatic pain is a form of pain with no known physical cause. This type of pain is largely driven by feelings of depression and anxiety, along with various other biopsychosocial factors.

Kratom FAQs
Kratom is one of the leading herbs used for pain relief around the world. It offers all the benefits of opiate painkillers without the negative side effects.
The following FAQs provide more information about kratom for treating pain and its potential uses and risks:
What is Kratom?
Kratom (Mitragyna speciosa) is a tropical tree native to Southeast Asia. The leaves of the tree have been used for centuries in traditional medicine as a natural pain reliever and energizer.
What is Kratom Used For?
Kratom is a member of the coffee family of plants (Rubiaceae). As such, kratom shares similar chemical properties to other members of the family, including the coffee plant (Coffea arabica).
For example, kratom contains a series of xanthine alkaloids similar to caffeine in coffee that act as central nervous system stimulants.
Laborers living in Thailand, Vietnam, and Indonesia would chew the leaves as they worked to offset feelings of fatigue and improve productivity. Kratom is still used today in lower doses for this effect and can be viewed as a coffee alternative.
In higher doses, the effects of kratom take a complete U-turn, producing feelings of calmness and analgesia. It numbs the body along with many different forms of pain.

How Does Kratom Work For Pain?
Kratom contains compounds called alkaloids, which interact with receptors in the brain to produce pain-relieving effects. The specific alkaloids in kratom that are believed to be responsible for its pain-relieving effects are called mitragynine and 7-hydroxymitragynine.
Is Kratom Legal?
Kratom is legal in most parts of the world — but there are a few exceptions.
In the United States, kratom is not a controlled substance but has been banned in several states (Alabama, Indiana, Rhode Island, New Hampshire, Tennessee, Vermont, and Wisconsin).
In Canada, kratom is legal and tightly regulated by the Canadian Food Inspection Agency (CFIA).
In Europe, the legality of kratom varies substantially. Currently, kratom is banned in the United Kingdom, Germany, France, Denmark, Sweden, and Italy.
Will Kratom Make Me Fail a Drug Test?
It’s possible, but very unlikely, for kratom users to fail a standard 12-panel drug test. Certain drug tests can detect the presence of alkaloids in kratom, such as mitragynine and 7-hydroxymitragynine. However, it’s uncommon for kratom to be included on the list of substances drug tests search for.
How Long Does the Pain-Relief From Kratom Last?
The duration of pain relief from kratom may vary depending on several factors — including the strain used, the dose, the individual’s metabolism, the type of pain being treated, and several other factors.
In general, users can expect kratom to take about 15 to 30 minutes to kick in and about 2 hours of peak analgesic action. This is followed by around 2–3 hours of gradually weaning pain relief as the alkaloids are metabolized, and the effects wear off.
Is Kratom Safe to Use For Pain Relief?
Any substance that has a strong impact on the body carries some risk of side effects.
With kratom, the biggest risks come from taking very high doses or mixing kratom with other medications.
High doses of kratom can cause users to feel nauseous and dizzy. It may even make them throw up.
These side effects are uncomfortable but are what makes kratom so much safer to use than prescription opioids. Taking too much kratom is very uncomfortable but very rarely fatal. Prescription opioids, however, killed as many as 69,000 people in the US alone in 2020.
To use kratom for pain safely, it’s important to strive to take the lowest effective dose possible (rather than doubling down just for good measure), avoid mixing it with any of your prescription medications (unless otherwise specified by a doctor) and apply other concomitant therapies that target the underlying cause of the condition. The goal shouldn’t be to use kratom forever — rather, take it as a tool to improve one’s quality of life while the cause of the problem can be addressed effectively.
- Eastlack, S. C., Cornett, E. M., & Kaye, A. D. (2020). Kratom—Pharmacology, clinical implications, and outlook: a comprehensive review. Pain and therapy, 9(1), 55-69.
- Rosenblum, A., Marsch, L. A., Joseph, H., & Portenoy, R. K. (2008). Opioids and the treatment of chronic pain: controversies, current status, and future directions. Experimental and clinical psychopharmacology, 16(5), 405.
- Chen, L., Huang, Y., Yu, X., Lu, J., Jia, W., Song, J., … & Li, M. (2021). Corynoxine protects dopaminergic neurons through inducing autophagy and diminishing neuroinflammation in rotenone-induced animal models of Parkinson’s disease. Frontiers in pharmacology, 12, 642900.
- Chittrakarn, S., Keawpradub, N., Sawangjaroen, K., Kansenalak, S., & Janchawee, B. (2010). The neuromuscular blockade produced by pure alkaloid, mitragynine and methanol extract of kratom leaves (Mitragyna speciosa Korth.). Journal of ethnopharmacology, 129(3), 344-349.
- Ellis, C. R., Racz, R., Kruhlak, N. L., Kim, M. T., Zakharov, A. V., Southall, N., … & Stavitskaya, L. (2020). Evaluating kratom alkaloids using PHASE. PloS one, 15(3), e0229646.
- Kruegel, A. C., Gassaway, M. M., Kapoor, A., Váradi, A., Majumdar, S., Filizola, M., … & Sames, D. (2016). Synthetic and receptor signaling explorations of the mitragyna alkaloids: mitragynine as an atypical molecular framework for opioid receptor modulators. Journal of the American Chemical Society, 138(21), 6754-6764.
- Todd, D. A., Kellogg, J. J., Wallace, E. D., Khin, M., Flores-Bocanegra, L., Tanna, R. S., … & Cech, N. B. (2020). Chemical composition and biological effects of kratom (Mitragyna speciosa): In vitro studies with implications for efficacy and drug interactions. Scientific reports, 10(1), 1-13.
- Vicknasingam, B., Chooi, W. T., Rahim, A. A., Ramachandram, D., Singh, D., Ramanathan, S., … & Chawarski, M. C. (2020). Focus: Plant-based medicine and pharmacology: Kratom and pain tolerance: A randomized, placebo-controlled, double-blind study. The Yale Journal of Biology and Medicine, 93(2), 229.
- Campbell, J. N., & Meyer, R. A. (2006). Mechanisms of neuropathic pain. Neuron, 52(1), 77-92.
- Nacca, N., Schult, R. F., Li, L., Spink, D. C., Ginsberg, G., Navarette, K., & Marraffa, J. (2020). Kratom adulterated with phenylethylamine and associated intracerebral hemorrhage: linking toxicologists and public health officials to identify dangerous adulterants. Journal of medical toxicology, 16(1), 71-74.
- Popkirov, S., Enax-Krumova, E. K., Mainka, T., Hoheisel, M., & Hausteiner-Wiehle, C. (2020). Functional pain disorders–more than nociplastic pain. NeuroRehabilitation, 47(3), 343-353.
- Utar, Z., Majid, M. I. A., Adenan, M. I., Jamil, M. F. A., & Lan, T. M. (2011). Mitragynine inhibits the COX-2 mRNA expression and prostaglandin E2 production induced by lipopolysaccharide in RAW264. 7 macrophage cells. Journal of Ethnopharmacology, 136(1), 75-82.
- Suhaimi, F. W., Yusoff, N. H., Hassan, R., Mansor, S. M., Navaratnam, V., Müller, C. P., & Hassan, Z. (2016). Neurobiology of Kratom and its main alkaloid mitragynine. Brain research bulletin, 126, 29-40.
- Goel, A., Boland, C. R., & Chauhan, D. P. (2001). Specific inhibition of cyclooxygenase-2 (COX-2) expression by dietary curcumin in HT-29 human colon cancer cells. Cancer letters, 172(2), 111-118.
- Lydecker, A. G., Sharma, A., McCurdy, C. R., Avery, B. A., Babu, K. M., & Boyer, E. W. (2016). Suspected adulteration of commercial kratom products with 7-hydroxymitragynine. Journal of Medical Toxicology, 12(4), 341-349.
- LeSaint, K. T., Yin, S., Sharma, A., Avery, B. A., McCurdy, C. R., & Waksman, J. C. (2022). Acute Renal Insufficiency Associated With Consumption of Hydrocodone-and Morphine-Adulterated Kratom (Mitragyna Speciosa). Journal of Emergency Medicine, 63(1), e28-e30.
- Eastlack, S. C., Cornett, E. M., & Kaye, A. D. (2020). Kratom—Pharmacology, clinical implications, and outlook: a comprehensive review. Pain and therapy, 9(1), 55-69.
- Foss, J. D., Nayak, S. U., Tallarida, C. S., Farkas, D. J., Ward, S. J., & Rawls, S. M. (2020). Mitragynine, bioactive alkaloid of kratom, reduces chemotherapy-induced neuropathic pain in rats through α-adrenoceptor mechanism. Drug and alcohol dependence, 209, 107946.
- Harun, N., Hassan, Z., Navaratnam, V., Mansor, S. M., & Shoaib, M. (2015). Discriminative stimulus properties of mitragynine (kratom) in rats. Psychopharmacology, 232(13), 2227-2238.
- Hiranita, T., Leon, F., Felix, J. S., Restrepo, L. F., Reeves, M. E., Pennington, A. E., … & Wilkerson, J. L. (2019). The effects of mitragynine and morphine on schedule-controlled responding and antinociception in rats. Psychopharmacology, 236(9), 2725-2734.
- Matsumoto, K., Mizowaki, M., Suchitra, T., Murakami, Y., Takayama, H., Sakai, S. I., … & Watanabe, H. (1996). Central antinociceptive effects of mitragynine in mice: contribution of descending noradrenergic and serotonergic systems. European journal of pharmacology, 317(1), 75-81.
- Hemby, S. E., McIntosh, S., Leon, F., Cutler, S. J., & McCurdy, C. R. (2019). Abuse liability and therapeutic potential of the Mitragyna speciosa (kratom) alkaloids mitragynine and 7‐hydroxymitragynine. Addiction Biology, 24(5), 874-885.
- Kruegel, A. C., Uprety, R., Grinnell, S. G., Langreck, C., Pekarskaya, E. A., Le Rouzic, V., … & Sames, D. (2019). 7-Hydroxymitragynine is an active metabolite of mitragynine and a key mediator of its analgesic effects. ACS central science, 5(6), 992-1001.
- Takayama, H., Ishikawa, H., Kurihara, M., Kitajima, M., Aimi, N., Ponglux, D., … & Horie, S. (2002). Studies on the synthesis and opioid agonistic activities of mitragynine-related indole alkaloids: discovery of opioid agonists structurally different from other opioid ligands. Journal of medicinal chemistry, 45(9), 1949-1956.
- Spetea, M., & Schmidhammer, H. (2019). Unveiling 7-Hydroxymitragynine as the Key Active Metabolite of Mitragynine and the Promise for Creating Novel Pain Relievers.
- Shi, J. S., Yu, J. X., Chen, X. P., & Xu, R. X. (2003). Pharmacological actions of Uncaria alkaloids, rhynchophylline and isorhynchophylline. Acta Pharmacologica Sinica, 24(2), 97-101.
- Kang, T. H., Murakami, Y., Matsumoto, K., Takayama, H., Kitajima, M., Aimi, N., & Watanabe, H. (2002). Rhynchophylline and isorhynchophylline inhibit NMDA receptors expressed in Xenopus oocytes. European journal of pharmacology, 455(1), 27-34.
- Roquebert, J., & Demichel, P. (1984). Inhibition of the α1-and α2-adrenoceptor-mediated pressor response in pithed rats by raubasine, tetrahydroalstonine and akuammigine. European journal of pharmacology, 106(1), 203-205.
- Matsumoto, K., Takayama, H., Ishikawa, H., Aimi, N., Ponglux, D., Watanabe, K., & Horie, S. (2006). Partial agonistic effect of 9-hydroxycorynantheidine on μ-opioid receptor in the guinea-pig ileum. Life sciences, 78(19), 2265-2271.
- Obeng, S., Kamble, S. H., Reeves, M. E., Restrepo, L. F., Patel, A., Behnke, M., … & McCurdy, C. R. (2019). Investigation of the adrenergic and opioid binding affinities, metabolic stability, plasma protein binding properties, and functional effects of selected indole-based kratom alkaloids. Journal of medicinal chemistry, 63(1), 433-439.
- Doxey, J. C., Lane, A. C., Roach, A. G., & Virdce, N. K. (1984). Comparison of the α-adrenoceptor antagonist profiles of idazoxan (RX 781094), yohimbine, rauwolscine and corynanthine. Naunyn-Schmiedeberg’s archives of pharmacology, 325(2), 136-144.
- Utar, Z., Majid, M. I. A., Adenan, M. I., Jamil, M. F. A., & Lan, T. M. (2011). Mitragynine inhibits the COX-2 mRNA expression and prostaglandin E2 production induced by lipopolysaccharide in RAW264. 7 macrophage cells. Journal of Ethnopharmacology, 136(1), 75-82.
- Chen, L. L., Song, J. X., Lu, J. H., Yuan, Z. W., Liu, L. F., Durairajan, S. S. K., & Li, M. (2014). Corynoxine, a natural autophagy enhancer, promotes the clearance of alpha-synuclein via Akt/mTOR pathway. Journal of Neuroimmune Pharmacology, 9(3), 380-387.
- Vicknasingam, B., Chooi, W. T., Rahim, A. A., Ramachandram, D., Singh, D., Ramanathan, S., … & Chawarski, M. C. (2020). Focus: Plant-based medicine and pharmacology: Kratom and pain tolerance: A randomized, placebo-controlled, double-blind study. The Yale Journal of Biology and Medicine, 93(2), 229.
- Kang, T. H., Matsumoto, K., Tohda, M., Murakami, Y., Takayama, H., Kitajima, M., … & Watanabe, H. (2002). Pteropodine and isopteropodine positively modulate the function of rat muscarinic M1 and 5-HT2 receptors expressed in Xenopus oocyte. European journal of pharmacology, 444(1-2), 39-45.
- Sabbir, M. G., & Fernyhough, P. (2018). Muscarinic receptor antagonists activate ERK-CREB signaling to augment neurite outgrowth of adult sensory neurons. Neuropharmacology, 143, 268-281.
- Ward, R. P., & Dorsa, D. M. (1996). Colocalization of serotonin receptor subtypes 5-HT2A, 5-HT2C, and 5‐HT6 with neuropeptides in rat striatum. Journal of Comparative Neurology, 370(3), 405-414.
- Ruiz-Martel, C., Doroteo-Ortega, V. H., González-Aspajo, G., Deharo, E., Alban-Castillo, J., Robert, G., … & Bourdy, G. (2012). Anti-inflammatory activity of Mitraphylline isolated from Uncaria tomentosa bark.
- Rojas-Duran, R., González-Aspajo, G., Ruiz-Martel, C., Bourdy, G., Doroteo-Ortega, V. H., Alban-Castillo, J., … & Deharo, E. (2012). Anti-inflammatory activity of Mitraphylline isolated from Uncaria tomentosa bark. Journal of Ethnopharmacology, 143(3), 801-804.
- Rojas-Duran, R., González-Aspajo, G., Ruiz-Martel, C., Bourdy, G., Doroteo-Ortega, V. H., Alban-Castillo, J., … & Deharo, E. (2012). Anti-inflammatory activity of Mitraphylline isolated from Uncaria tomentosa bark. Journal of Ethnopharmacology, 143(3), 801-804.
- Qu, Z., Liu, A., Li, P., Liu, C., Xiao, W., Huang, J., … & Zhang, S. (2021). Advances in physiological functions and mechanisms of (−)-epicatechin. Critical reviews in food science and nutrition, 61(2), 211-233.
- Quiñonez-Bastidas, G. N., Pineda-Farias, J. B., Flores-Murrieta, F. J., Rodríguez-Silverio, J., Reyes-García, J. G., Godínez-Chaparro, B., … & Rocha-González, H. I. (2018). Antinociceptive effect of (−)-epicatechin in inflammatory and neuropathic pain in rats. Behavioural Pharmacology, 29(2), 270-279.
- Safayhi, H., Boden, S. E., Schweizer, S., & Ammon, H. P. (2000). Concentration-Dependent Potentiating and Inhibitory Effects of Boswellia Extracts on 5-Lipoxygenase Product Formation inStimulated PMNL. Planta medica, 66(02), 110-113.
- Liao, Y., Guo, C., Wen, A., Bai, M., Ran, Z., Hu, J., … & Ding, Y. (2023). Frankincense-Myrrh treatment alleviates neuropathic pain via the inhibition of neuroglia activation mediated by the TLR4/MyD88 pathway and TRPV1 signaling. Phytomedicine, 108, 154540.
- Rondanelli, M., Fossari, F., Vecchio, V., Gasparri, C., Peroni, G., Spadaccini, D., … & Perna, S. (2020). Clinical trials on pain lowering effect of ginger: A narrative review. Phytotherapy Research, 34(11), 2843-2856.
- Lanhers, M. C., Fleurentin, J., Mortier, F., Vinche, A., & Younos, C. (1992). Anti-inflammatory and analgesic effects of an aqueous extract of Harpagophytum procumbens. Planta Medica, 58(02), 117-123.
- Vlachojannis, J., Roufogalis, B. D., & Chrubasik, S. (2008). Systematic review on the safety of Harpagophytum preparations for osteoarthritic and low back pain. Phytotherapy research: PTR, 22(2), 149-152.
- Lim, D. W., Kim, J. G., Lim, E. Y., & Kim, Y. T. (2018). Antihyperalgesic effects of ashwagandha (Withania somnifera root extract) in rat models of postoperative and neuropathic pain. Inflammopharmacology, 26(1), 207-215.
- Mlost, J., Bryk, M., & Starowicz, K. (2020). Cannabidiol for pain treatment: focus on pharmacology and mechanism of action. International journal of molecular sciences, 21(22), 8870.
- Cosentino, M., Legnaro, M., Luini, A., Ferrari, M., Sodergren, M., Pacchetti, B., & Marino, F. (2022). Effect of Cannabidiol on Cyclooxygenase Type 1 and 2 Expression and Function in Human Neutrophils. Cannabis and Cannabinoid Research.
- Blake, D. R., Robson, P., Ho, M., Jubb, R. W., & McCabe, C. S. (2006). Preliminary assessment of the efficacy, tolerability and safety of a cannabis-based medicine (Sativex) in the treatment of pain caused by rheumatoid arthritis. Rheumatology, 45(1), 50-52.
- Barnes, M. P. (2006). Sativex®: clinical efficacy and tolerability in the treatment of symptoms of multiple sclerosis and neuropathic pain. Expert opinion on pharmacotherapy, 7(5), 607-615.
- Johnson, J. R., Burnell-Nugent, M., Lossignol, D., Ganae-Motan, E. D., Potts, R., & Fallon, M. T. (2010). Multicenter, double-blind, randomized, placebo-controlled, parallel-group study of the efficacy, safety, and tolerability of THC: CBD extract and THC extract in patients with intractable cancer-related pain. Journal of pain and symptom management, 39(2), 167-179.
- Serpell, M., Ratcliffe, S., Hovorka, J., Schofield, M., Taylor, L., Lauder, H., & Ehler, E. (2014). A double‐blind, randomized, placebo‐controlled, parallel group study of THC/CBD spray in peripheral neuropathic pain treatment. European journal of pain, 18(7), 999-1012.
- Borgonovo, G., De Petrocellis, L., Schiano Moriello, A., Bertoli, S., Leone, A., Battezzati, A., … & Bassoli, A. (2020). Moringin, a stable isothiocyanate from Moringa oleifera, activates the somatosensory and pain receptor TRPA1 channel in vitro. Molecules, 25(4), 976.
- Hedberg, M. H., Linnanen, T., Jansen, J. M., Nordvall, G., Hjorth, S., Unelius, L., & Johansson, A. M. (1996). 11-substituted (R)-aporphines: synthesis, pharmacology, and modeling of D2A and 5-HT1A receptor interactions. Journal of medicinal chemistry, 39(18), 3503-3513.
- Wen, H., Zhou, S., Li, J., Peng, F., Han, X., & Li, H. (2021). Nuciferine attenuates the progression of osteoarthritis by targeting PI3K/Akt/NF-κB signaling pathway. Journal of Functional Foods, 86, 104682.
- Nawrot, J., Napierała, M., Kaczerowska-Pietrzak, K., Florek, E., Gornowicz-Porowska, J., Pelant, E., & Nowak, G. (2019). The Anti-Serotonin Effect of Parthenolide Derivatives and Standardised Extract from the Leaves of Stizolophus balsamita. Molecules, 24(22), 4131.
- Dell’Agli, M., Galli, G. V., Bosisio, E., & D’Ambrosio, M. (2009). Inhibition of NF-kB and metalloproteinase-9 expression and secretion by parthenolide derivatives. Bioorganic & medicinal chemistry letters, 19(7), 1858-1860.
- Barsby RW, Salan U, Knight DW, Hoult JR. (1992). Feverfew extracts and parthenolide irreversibly inhibit vascular responses of the rabbit aorta. J Pharm Pharmacol. 44:737–40.
- Schmidt, K. L., & Simon, E. (2001). Thermotherapy of pain, trauma, and inflammatory and degenerative rheumatic diseases. In Thermotherapy for neoplasia, inflammation, and pain (pp. 527-539). Springer, Tokyo.
- Patil, S., Sen, S., Bral, M., Reddy, S., Bradley, K. K., Cornett, E. M., … & Kaye, A. D. (2016). The role of acupuncture in pain management. Current pain and headache reports, 20(4), 1-8.
- Tsuchiya, M., Sato, E. F., Inoue, M., & Asada, A. (2007). Acupuncture enhances generation of nitric oxide and increases local circulation. Anesthesia & Analgesia, 104(2), 301-307.
- Manheimer, E., White, A., Berman, B., Forys, K., & Ernst, E. (2005). Meta-analysis: acupuncture for low back pain. Annals of internal medicine, 142(8), 651-663.
- Ju, Z. Y., Wang, K., Cui, H. S., Yao, Y., Liu, S. M., Zhou, J., … & Xia, J. (2017). Acupuncture for neuropathic pain in adults. Cochrane Database of Systematic Reviews, (12).
- Manheimer, E., Cheng, K., Linde, K., Lao, L., Yoo, J., Wieland, S., … & Bouter, L. M. (2010). Acupuncture for peripheral joint osteoarthritis. Cochrane database of systematic reviews, (1).
- Kuffler, D. P. (2019). Variables affecting the potential efficacy of PRP in providing chronic pain relief. Journal of pain research, 12, 109.
- Martínez-López, E. J., Hita-Contreras, F., Moral-García, J. E., Grao-Cruces, A., Ruiz, J. R., Redecillas-Peiró, M. T., & Martínez-Amat, A. (2015). Association of low weekly physical activity and sedentary lifestyle with self-perceived health, pain, and well-being in a Spanish teenage population. Science & Sports, 30(6), 342-351.
- Auvinen, J., Tammelin, T., Taimela, S., Zitting, P., & Karppinen, J. (2008). Associations of physical activity and inactivity with low back pain in adolescents. Scandinavian journal of medicine & science in sports, 18(2), 188-194.